The Radical Sign

You have learned that numbers can be obtained by raising rational numbers to integral exponents.

For example

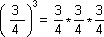
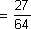
When the exponent is 2 we get squares or square numbers, the number which is raised by the exponent 2 is called the square root of the square so obtained.

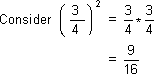
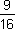
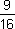          is the square of and is the square root of

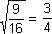  We write the square root as .

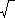  The symbol is called the radical.

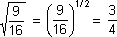  We can also write or the radical sign can be written as the power exponent of 1/2.

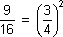   We have

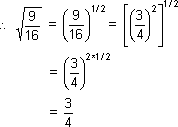
In this section we will be dealing with squares, perfect square numbers, and how to find the square roots of squares using

1. the prime factorization method

2. the division method.

Perfect Squares

If m and n are natural numbers such that n = m2 then n is the square of m and m is the square root of n.

For example,

4 = 2* 2 = 2²

4 is the square of 2

2 is the square root of 4.

The square of any integer is called a perfect square.

Consider the following table

Number	Square
1	12 = 1 *  1 = 1
2	22 = 2 *  2 = 4
3	32 = 3 * 3 = 9
4	42 = 4 *4 = 16
5	52 = 5 *5 = 25
6	62 = 6 * 6 = 36
7	72 = 7 * 7 = 49
8	82 = 8 * 8 = 64
9	92 = 9 * 9 = 81
10	102 = 10 * 10 = 100
11	112= 11 * 11 = 121
12	122 = 12 * 12 = 144
13	132 = 13 * 13 = 169
14	142 = 14 * 14 = 196
15	152 = 15 * 15 = 225
16	162 = 16 * 16 = 256
17	172 = 17 * 17 = 289
18	182 = 18 * 18 = 324
19	192 = 19 * 19 = 361
20	202 = 20 * 20 = 400

Properties of Square Numbers:

1. No square number has a units digit of 2, 3, 7, or 8. Check the table or your calculator. Choose any number and
   find its square. Its units digit will never be 2, 3, 7, or 8. So any number with 2, 3, 7, or 8 as the units digit is
   never a perfect square.




2. Given the units digit of a number, we can determine the units digit of its square.

   A number with units digit 1 or 9 has a square with units digit 1.

   A number with units digit 2 or 8 has a square with units digit 4.

   A number with units digit 3 or 7 has a square with units digit 9.

   A number with units digit 4 or 6 has a square with units digit 6.

   A number with units digit 5 or 0 has a square with units digit 5 or 0.




3. The number of zeros at the end of a perfect square is always even. If a number has 0 as its units digit for example
   20, its square 400 ends in double zero. If it has two zeros at the end as in 400 its square has four zeros 160000.
   So the square of a number always has double number of zeros at the end of its square. A number ending with
   an odd number of zeros is never a perfect square example 4000.

4. If a number is even or odd then so is its square as in 6² = 36, 7² = 49.

5. A perfect square leaves a remainder of 0 or 1 on division by 3.

6. If n is a perfect square, then 2n can never be a perfect square.

For example, 81 is a perfect square. 2* 81 = 162 is not a perfect square.

VIII. The number 1, 11, 111 …. have special properties.

1. 1² = 1

   11² = 1 2 1

   111² = 1 2 3 2 1

   1111² = 1 2 3 4 3 2 1

   -- = ----------

   111111111² = 1 2 3 4 5 6 7 8 9 8 7 6 5 4 3 2 1




2. 1² = 1

   11² = 1 2 1 and 1 + 2 + 1 = 4 = 2²

   111² = 1 2 3 2 1 and 1 + 2 + 3 + 2 + 1 = 9 = 3²

   -- = --------

   111111111² = 1 2 3 4 5 6 7 8 9 8 7 6 5 4 3 2 1

   and 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 81 = 9²




3. 121 * (1 + 2 + 1) = 121 * 4 = 484 = 22²

   12321 * (1 + 2 + 3 + 2 + 1) = 12321 * 9 = 110889 = 333²

   12345678987654321* (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 +1)

   = 999999999²

Check the above on your calculator.

Example 1

Check and see if any of the given numbers is a perfect square. Give one reason why it isn't a perfect square.

a) 33453     b) 52698     c) 99880

Solution:

	Reason:
a) 33453 is not a perfect square.        b) 52698 is not a perfect square.        c) 99880 is not a perfect square.	Its units digit is 3. Its units digit is 8. Its units digit is a single zero.

Try these problems

1. Which of the following numbers are perfect squares? Give a reason for you answer.

   1. 21222

   2. 576

   3. 7928




2. Observe the following patterns and fill in the missing digits.

   1. 11²= 1 2 1

      101² = 10201

      1001² = 1002001

      100001² = 1 _ _ _ 2 _ _ _ 1

      10000001²= _ _ _ _ _ _ _ _ _ _ _

   
   

   2. 11² = 121

      101² = 10201

      10101² = 102030201

      1010101² = -----------------------

      _____________² = 10203040504030201

   
   

   3. 1² + 2² + 2² = 3²

      2² + 3² + 6² = 7²

      3² + 4² + 12² = 13²

      4² + 5² + __² = 21²

      5² + _² + 30² = 31²

      6² + 7² + __² = __²

   
   

   4. 

      




3. Using the column method find the squares of

      a) 54      b) 95     c) 49




4. 1.  Find the smallest number by which 2028 must be divided so that it becomes a perfect square.
      Find the square root of the number so obtained.

   2.  Find the least number by which 4851 must be multiplied so that the product becomes a perfect square.
      Find the square root of the number so obtained.




5. 1. Find the least number that must be subtracted from 26535 to make it a perfect square.

   2. Find the least number that must be added to 15520 to make it a perfect square.

Answers to problems

1. 1. 21222 is not a perfect square, its units digit is 2.

   2. 576 is a perfect square, its units digit is 6.

   3. 7928 is not a perfect square. Its units digit is 8.




2. 1. Following the given pattern.

      100000012 = 1 0 0 0 0 2 0 0 0 0 1

      Notice that the blanks should contain the same number of zeros as the given number of zeros.

   
   

   2. Following the given pattern.

      10101012 = 1020304030201

      1010101012 = 10203040504030201

      Note that the values 1, 2, 3, 4 depend on the number of 1's in the given number alternating with the zeros.

   
   

   3. 4² + 5² + 20² = 21²

      5² + 6²+ 30² = 31²

      6² + 7² + 42² = 43²

      On the left-hand side, the product of the first two numbers give us the third number. On the right-hand side, the number is one more than the product of the first two numbers of the left-hand side.

   
   

   4. 

      
      

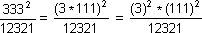
             See properties of square numbers.

      =9

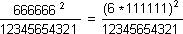        See properties of square numbers.

      
      

      

      
      
3. 
   

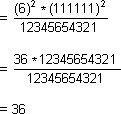
   a.	I x2	II 2xy	III y2	Check examples for reason
   	52	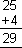2 * 5 *  4	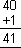42 16

   
   

   (54)² = 2916

   b. 95

   I x2	II 2xy	III y2
   92	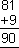2 *9 * 5	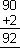52 25

   
   

   (95)² = 9025

   
   

   c. 49

   
   

   I x2	II 2xy	III y2
   42	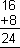2 * 4 * 9	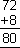92 81

   
   

   (49)²= 2401.




4. 1. We first use prime factorization.

      

      
      

      

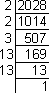
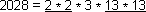
      3 is not a part of a pair. So 3 is the least number by which 2028 must be multiplied to get
      a perfect square.

      2028 * 3 = 6084

      

   
   

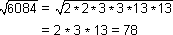
   2. We first use prime factorization

      

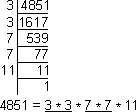
      11 is the only number which is not part of a pair. So 11 is the least number by which we need to divide
      4851 to obtain a perfect square.

      





5. 1. 

      
      

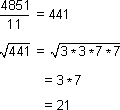
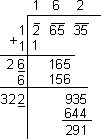
      291 is the least number to be subtracted from 26535 to make it a perfect square.

   
   

   2. 

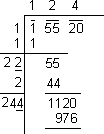
      976 is less than 1120.

      Repeating the process

      
      

      

      
      

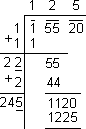
      The difference of 1225 and 1120 gives us the required

      number 1225 – 1120 = 105.

      The least number to be added to 1120 to make it a perfect square is 105.