Steps in Finding the Domain of a Rational Expression

1. Set the denominator of the rational expression equal to zero.

2. Solve for the variable present in the numerator.

3. The values for the variables we get in the above steps make the function undefined, so all the values other
   than these values are the domain of the rational expression.

Example: 1

Find the domain and range of f(x) = -4/x.

Solution:

The denominator becomes 0 when x=0; hence the domain is (-∞,0) U (0,∞) where (-∞,0) means that both -∞ and 0
are not included in the domain of x but the values between them are included. This is indicated by the brackets '('
and ')'.

Range = all nonzero real numbers.

Example : 2

Find the domain of the rational expression 3 / (2x2+7x-4).

Solution:

We put the denominator equal to zero, 2x2+7x-4=0,

and now solve the equation for x by factorizing the above quadratic equation.

p+q=7 and pq=-8; It's easy to figure out that p and q are 8 and -1.

                2x2+8x -x -4=0

• 2x(x+4)-1(x+4)=0

• (x+4)(2x-1)=0

x=1/2, -4 makes the expression undefined. Therefore, the values other than these values are the domain of the
expression,

i.e. -∞ < x < -4 or -4 < x < 1/2 or x > 1/2.

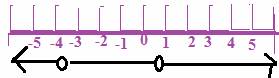
So the domain is (-∞, -4) U (-4, 1/2) U (1/2, ∞).

Try these problems

1. Find the domain of the function given below:

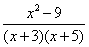   x > -3 and x > -5

2. all real values except -5

3. x > 3

4. x >-5

Answer : B

Explanation :

       =        

=       

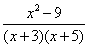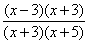
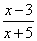
The domain of this simplified rational function can be determined by finding the value of x for which it is 0.

• X+5=0 when x = -5

The domain of the given rational function can have any value except -5.