Maxima, minima and zeros of quadratic functions Multiplication of Decimals
ZEROS
Let f(x) = ax2+bx+c represent a quadratic function.
If f(x) = 0
= ax2+bx+c = 0
Then, the roots of the quadratic equation are also called the zeros of the quadratic function.
MAXIMA
If f(x)=ax2+bx+c gradually increases until it reaches a value p, which is algebraically greater than its neighboring values on either side, then p is said to be the maximum value or maxima of f(x).
MINIMA
If f(x)= ax2+bx+c gradually increases until it reaches a value q, which is algebraically less than its neighboring values on either side, q is said to be the minimum value or minima of f(x).
These concepts can be visualized by drawing graphs.
Example : 1
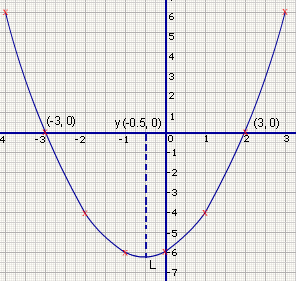
Draw the graph for x2+x-6 and find its zeros, maxima and minima, if they exist.
y = x2+x-6
| x |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
x2 |
16 |
9 |
4 |
1 |
0 |
1 |
4 |
9 |
x |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
-6 |
-6 |
-6 |
-6 |
-6 |
-6 |
-6 |
-6 |
-6 |
y |
-6 |
0 |
-4 |
-6 |
-6 |
-4 |
0 |
6 |
Plot the points (-4,6), (-3,0), (-2,-4), (-1,-6), (0,-6),(1,-4),(2,0),(3,6) and join them to form a smooth curve.
From the graph, the curve cuts the x-axis at (-3,0) and (2, 0).
So the zeros of x2+x-6 = 0 are x = -3,2.
The maxima does not exist, as the curve continues indefinitely on both sides.
The minima is obtained by drawing a line from point L to M on the x-axis.
LM=-6.25, which is the minimum value or minima and it occurs at x=-0.5.
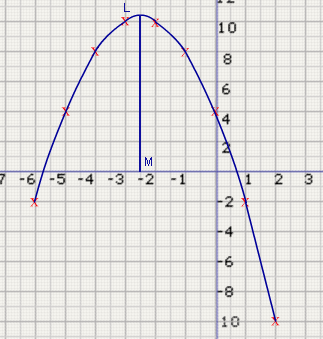
Try the following question
Draw the graph for the function f(x)= 4-5x-x2. From the graph obtain the zeros, maxima and minima, if they exist.
Let y = 4-5x-x2
x |
-6 |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
-x2 |
-36 |
-25 |
-16 |
-9 |
-4 |
-1 |
0 |
-1 |
-4 |
-5x |
30 |
25 |
20 |
15 |
10 |
5 |
0 |
-5 |
-10 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
y |
-2 |
4 |
8 |
10 |
10 |
8 |
4 |
-2 |
-10 |
Plot the points (-6,-2), (-5,4),(-4,8),(-3,10),(-2,10),(-1,8), (0,4),(1,-2),(2,-10) and join them to form a smooth curve.
From the graph, we see that the curve cuts the x-axis at the points (-5.7,0) and (0.7,0). So the zeros of 4-5x-x2 = 0 are x = -5.7, 0.7
Let L be the point where the curve is maximum. Drop a perpendicular from L to the x-axis, meeting the x-axis at M.
LM = 10.25. This is the maximum value and it occurs at
x = -2.5.
There is no minimum value as the curve continues on indefinitely on both sides.