Rules for Division

1. Like signs; positive
2. Unlike signs; negative

Multiplicative Inverse Property

Remember that when you divide fractions, you change the division problem to a multiplication problem and multiply by the reciprocal or multiplicative inverse.

Numbers that are reciprocals or multiplicative inverses are numbers whose product is one.

Examples

Reasoning
2/3 and 3/2   2/3(3/2) = 1	5/4 and 4/5   5/4(4/5) = 1	5 and 1/5   5/1(1/5) = 1	Change an integer into a fraction by putting it over one

Multiplicative Inverse Property:

For every nonzero number a, there is a 1/a so

a(1/a) = 1 or 1/a(a) = 1

Examples

Reasoning
25/5 = 5 -25/-5 = 5	Like signs; positive
24/-8 = -3 -24/8 = -3	Unlike signs; negative

Remember to use your rules to find the sign of your answer first.

Suggestion: In a division of fractions problem, if one of the numbers is not a fraction, make it a fraction by putting it over one.

Examples

Reasoning
-2/3 / 4	Make 4 a fraction by putting it over one
-2/3 / 4/1	Multiply by the reciprocal 1/4
-12/3 / 1/42	Unlike signs; negative Reduce 2 into 4 twice
-1/6	Multiply 1/3(1/2) = 1/6

When multiplying fractions, you multiply numerators and numerators and denominators and denominators.

Reasoning
-6 /  -3/8	Make the -6 a fraction by putting it over one
-6/1 / -3/8	Multiply by the reciprocal -8/3
-26/1 / -8/13	Like signs; positive Reduce 3 into 6 twice
16	Multiply (2/1)(8/1) = 16/1 = 16

Complex Fractions

There are even more complex fractions where the numerator, the denominator, or both are fractions. These fractions are in fact called complex fractions.

Examples

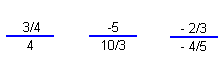
To divide complex fractions, rewrite as a division of fractions problem with the becoming the division sign.

Examples

Reasoning
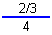
	Rewrite as a division of fractions problem.
2/3 / 4/1	Place the 4 over one Multiply by the reciprocal 1/4
12/3 / 1/42	Like signs; positive Reduce 2 into 4 twice
1/6	Multiply 1/3(1/2) = 1/6

Reasoning
	Rewrite as a division of fractions problem
-5/1 / 10/3	Place the five over one Multiply by the reciprocal 3/10
-15/1 / 3/102	Unlike signs; negative Reduce 5 into 10 twice
-3/2	Multiply 1/1(3/2) = 3/2

Reasoning
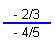
	Rewrite as a division of fractions problem
-2/3 / -4/5	Multiply by the reciprocal -5/4
-12/3 / -5/42	Like signs; positive Reduce 2 into 4 twice
5/6	Multiply 1/3(5/2) = 5/6

Not only can you use the distributive property for multiplication, but you can also use it for division.

Examples

Reasoning
	Since a fraction bar is a grouping symbol, this problem tells us to divide both the 3x and the 6 by 3
x + 2	3x/3 = x    the 3s will cancel 6/3 = 2

Reasoning
	Divide both
-2x + 3	10x/-5 = -2x    Unlike signs; negative and -15/-5 = 3    Like signs; positive

Simplify

1. -15/3


2. -30/-6


3. 56/8


4. 63/-9


5. Hint: To divide complex fractions, rewrite as a division of fractions problem with
   becoming the division sign.


6. Hint: To divide complex fractions, rewrite as a division of fractions problem with
   becoming the division sign.



7.   5x - 25  
        5




8.   -7x + 42  
        -7




9.   12x + 18  
        3



10. -12 / -3


11. -24 / 6

Answers to Practice Problems

1. -15/3 = -5
2. -30/-6 = 5
3. 56/8 = 7
4. 63/-9 = -7
5. -2/1 / 4/5
   -12/1 / 5/42
   -5/2
6. 7/8 / -6/1
   7/8 / -1/6
   -7/48
7. -2/3 / -4/9
   -12/31 / -39/42
   3/2

8.   5x - 25    =  x - 5
        5

9.   -7x + 42    =  x - 6
        -7

  12x + 18    =  4x + 6
     3
10. -12 / -3 = 4
11. -24 / 6 = -4