Functions

A relation is any set of ordered pairs.

A function is a set of ordered pairs where no two first values are the same.

To determine whether a set of ordered pairs is a function or a relation:

  1. Look at the first numbers in the ordered pairs
  2. If all of the first numbers are different, then the set of ordered pairs is a function
  3. If any two first numbers are the same, then the set of ordered pairs is a relation

Examples: Identify each set of ordered pairs as a relation or a function. List the domain and range.

Reasoning

  1. {(-4,3),(5,6),(-4,8),(5,-3)}
    Relation
    Domain: {-4,5}
    Range: {-3,3,6,8}
    Look at the first numbers or the
    x-values in the ordered pairs
    Since there are two -4s, and two 5s, the set of ordered pairs is a relation
    List the domain or x-values
    as {-4,5} because we list each number just once and in ascending order
    List the range or y-values
    as {-3,3,6,8} because we list the numbers in ascending order

  2. {(-2,6),(-1,5),(0,6),(1,5)}
    Function
    Domain: {-2,-1,0,1}
    Range: {5,6}
    Look at the first numbers or the
    x-values in the ordered pairs
    Since all the x-values are different, the set of ordered pairs is a function
    List the domain or x-values
    as {-2,-1,0,1} because we list the numbers in ascending order
    List the range or y-values
    as {5,6} because we list each number just once and in ascending order

Graphic representation of a function and a relation

We can also determine whether a graph represents a relation or a function by looking at the graph’s ordered pairs. In fact, we can tell whether a graph is a function or a relation by just looking at the graph. This is called the vertical line test.

If a vertical line passes through more than one point of a graph, then it is a relation.

If a vertical line does not pass through more than one point of a graph, then it is a function.

Reasoning: All ordered pairs on the same vertical line have the same x-value.

Example: Identify each graph as a function or a relation.


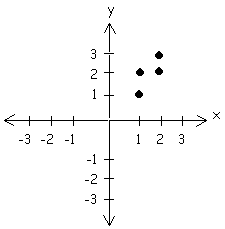
  1. Relation
    Reasoning
    The graph is a relation because we can draw a vertical line through more than one point


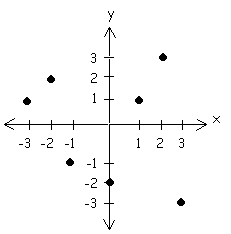
  2. Function
    Reasoning
    The graph is a function because any vertical line would pass through only one point

Function values of a function

Functions can also be expressed as equations. Because of that, we can find values of functions. The equations that we will work with will be of the form

y = ax + b and y = ax2 + bx + c.

When we are asked to find the value of a function, we express the functions as f(x) = ax + b and f(x) = ax2 + bx + c, where f(x) = y and tells us to find the value of the function (y) for the given value of x.

f(x) is read "f of x".

Examples: If f(x) = 2x - 5, find:

Reasoning

  1. f(2)
    f(2) = 2(2) - 5
    f(2) = 4 - 5
    f(2) = -1
    f(2) tells us to substitute 2 in for x and then simplify
    In 2(2) - 5, we multiply first to
    get 4 - 5 then add to get -1

  2. f(-3)
    f(-3) = 2(-3) - 5
    f(-3) = -6 - 5
    f(-3) = -11
    f(-3) tells us to substitute -3 in for x and then simplify
    In 2(-3) - 5, we multiply first to
    get -6 - 5 and then add to get -11

By finding the values of the function, we can express a set of ordered pairs because f(x) = y.

Since f(2) = -1, y = -1 for (2,-1)

Since f(-3) = -11, y = -11 for (-3,-11)

Remember: When raising a number to a power, the exponent tells us the sign of our answer. If the exponent is even, then the answer is positive. If the exponent is odd, then the answer is negative.

Example: If f(x) = x2 - 3x + 2, find

Reasoning

  1. f(-1)
    f(-1) = (-1)2 - 3(-1) + 2
    f(-1) = 1 + 3 + 2
    f(-1) = 6
    f(-1) tells us to substitute -1 in for x
    In (-1)2 - 3(-1) + 2, order of operations tells us to do the power and multiplication first 1 + 3 + 2 and then add to get 6

  2. f(4)
    f(4) = (4)2 - 3(4) + 2
    f(4) = 16 - 12 + 2
    f(4) = 6
    f(4) tells us to substitute 4 in for x and then simplify
    In (4)2 - 3(4) + 2, order of operations tells us to do the power and multiplication first 16 - 12 + 2 and then add to get 6

Determining the ordered pair solution of a function

A solution of a function is an ordered pair that makes a true sentence. As a result, we can tell whether an ordered pair is a solution by substituting the ordered pair into the equation and determining whether it makes a true sentence.

Example: Determine whether the following ordered pairs is a solution to y = 3x - 5:

Reasoning

  1. (-3,4)
    4 = 3(-3) - 5
    4 = -9 - 5
    4 ≠ -14
    (-3,4) is not a solution
    Substitute the 4 in for y and
    the -3 in for x
    Simplify by multiplying first
    3(-3) - 5 = -9 - 5 then adding
    -9 - 5 = -14
    4 is not equal to -14, so (-3,4) is not a solution

  2. (4,7)
    7=3(4)-5
    7=12-5
    7=7
    (4,7) is a solution
    substitute the 7 in for y and
    the 4 in for x
    Simplify by multiplying first
    3(4) - 5 = 12 - 5 then adding
    12 - 5 = 7
    7 is equal to 7, so (4,7) is a solution

Try these problems:

Identify if each set of ordered pairs is a relation or a function. List the domain and range.

  1. {(-3,8),(-2,5),(3,7),(5,-1)}
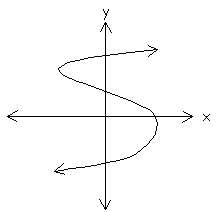
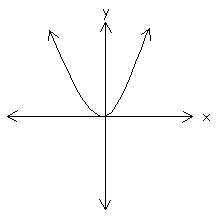
  2. {(4,3),(5,-2),(4,-4),(5,7)} Identify the following graphs as a relation or a function.

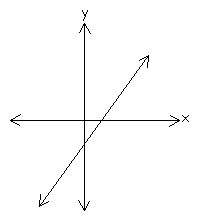
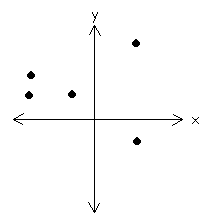
Identify if each set of ordered pairs is a relation or a function. List the domain and range.

  1. {(-3,8),(-2,5),(3,7),(5,-1)}
  2. {(4,3),(5,-2),(4,-4),(5,7)}
    Identify the following graphs as a relation or a function.

  5. Do the following tables represent a relation or a function? Express the table as a set of ordered pairs. List the domain and range.


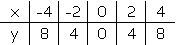
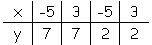
  7. Problem Solving
  8. If you have pieces of paper in one box with the numbers 0, 1, 2, 3, 4 and pieces of paper in a second box with the numbers 5, 6, 7, 8, 9, explain how you could form five ordered pairs that would represent a function. Explain your reasoning.

Answers to Practice Problems

  1. Function
    Domain: {-3,-2,3,5}
    Range: {-1,5,7,8}
  2. Relation
    Domain: {4,5}
    Range: {-4,-2,3,7}
  3. Function
  4. Relation
  5. Relation
  6. Function
  7. Relation
    {(-5,7),(3,7),(-5,2),(3,2)}
    Domain: {-5,3}
    Range: {2,7}
  8. To make sure that I would have five ordered pairs that represent a function, I would draw a number from the first box and then a number from the second box and pair them together. I would continue to do this until all five numbers from the first box are paired with a number from the second box.
    Find the value of the function f(x) = 2x - 5 for:
  1. f(-2) =
  2. f(0) =
    3. Find the value of the function f(x) = 2x2 - 4x + 7 for:
  3. f(-2) =
  4. f(0) =
    5. Determine if each ordered pair is a solution for y = -2x + 3:
  5. A = (-2,7)
  6. B = (3,6)
    7. Determine if each ordered pair is a solution for y = x2 - 2x + 3: D = (1,2) E = (-2,11)

Answers to Practice Problems

  1. f(-2) = 2(-2) - 5
    f(-2) = -4 - 5
    f(-2) = -9
  2. f(0) = 2(0) - 5
    f(0) = 0 - 5
    f(0) = -5

  3. f(-2) = 2(-2)2 - 4(-2) + 7
    f(-2) = 2(4) + 8 + 7
    f(-2) = 8 + 8 + 7
    f(-2) = 23

  4. f(0) = 2(0)2 - 4(0) + 7
    f(0) = 2(0) + 0 + 7
    f(0) = 0 + 0 + 7
    f(0) = 7

    5. Determine if each ordered pair is a solution for y = -2x + 3:

  5. A = (-2,7)
    7 = -2(-2) + 3
    7 = 4 + 3
    7 = 7
    (-2,7) is a solution

  6. B = (3,6)
    6 = -2(3) + 3
    6 = -6 + 3
    6 ≠ -3
    (3,6) is not a solution

    7. Determine if each ordered pair is a solution for y = x2 - 2x + 3:

  7. D = (1,2)
    2 = (1)2 - 2(1) + 3
    2 = 1 - 2 + 3
    2 = 2
    (1,2) is a solution

  8. E = (-2,11)
    11 = (-2)2 - 2(-2) + 3
    11 = 4 + 4 + 3
    11 = 11
    (-2,11) is a solution