Recall that a set is a well-defined collection of objects.
Examples:
a collection of flowers
{ Rose, Lily, Dahlia, Foxglove, Pentunia}
the set of natural numbers
N = { 1,2,3, ..............}
the set of integers
Z = { ........ -3,-2,-1,0,1,2,3, ............} etc.
The cartesian product of two sets A, B is A x B (read as A cross B), and is defined as
A x B= { (a,b) | a∈A, ∈B}
that is, A x B is a set of ordered pairs where the first coordinate belongs to the set A and the second
coordinate belongs to set B.
Consider this example.
Let A = {1,2,3} B = {-1,-2,3}
A x B = { (1,-1), (1,-2), (1,3), (2,-1), (2,-2), (2,3), (3,-1), (3,-2), (3,3) }.
If
n(A) = number of element in A = p
n(B) = number of elements in B = q
then n(A x B) = number of elements in A x B = p x q.
In the above case
n (A) = 3
n (B) = 3
n(A x B) = 3 x 3 = 9.
Consider these relations in mathematics.
-
a is equal to b or a=b
-
a is greater than b or a>b
-
line p is perpendicular to line q or p⊥ q
line x is parallel to y or x||y.
The symbols =, >,⊥ , || all denote specific relations. In general, we use R to denote a relation between two elements.
If x and y are in a relation, we denote it by x∈y or (x,y) ∈ R. If x and y are not in a relation, we denote this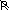 
by x y or (x,y)
∉R. Sets have elements that are ordered pairs. In other words, a relation is a set of ordered pairs.
The property that connects the coordinates of an ordered pair in a relation is the formula of a relation.
Observe the following relations. State the formula, if any, for each of the following relations.
-
R1={(1,1), (2,2), (3,3)}
-
R2={(1,2), (1,3), (2,3)}
-
R3={(3,2), (3,1), (2,1)}
-
The coordinates of every ordered pair in R1 are equal to each other.
The formula for R1 is "equal to" or (a,b) ∈R1 ⇒a = b.
-
The coordinates of every ordered pair in R2 are less than.
The formula for R2 is "less than" or (a,b) ∈R2 ⇒a < b.
-
The coordinates of every ordered pair in R3 are greater than.
The formula for R3 is "greater than" or (a,b) ∈R3 ⇒a > b.
The set of the first coordinates of all ordered pairs of a relation is called the Domain of R. The set of the second coordinates of all ordered pairs of R is called the Range of R.
Consider R = {(1,2), (2,3), (3,4), (4,5)}
Domain of R = Dom R={1,2,3,4}
Range of R = {2,3,4,5}.
If R is a relation from set A into another set B, then by interchanging the first and second coordinates of R we get a new relation from B into A. This is called the Inverse Relation of R and is denoted by R-1.
So (x,y) ∈R if and only if (y,x) ∈R-1
if R = {(x,y) | x ∈A, y ∈B}
then R-1 = {(y,x) | y ∈B, x ∈A}
Domain of R-1 = range of R = B.
Range of R-1 = domain of R = A.
If R is the relation "is less than" then R-1 is the relation "is greater than".
Let R = {(a,b), (c,d), (e,f), (l,m)}
R-1 = {(b,a), (d,c), (f,e), (m,l)}
If R = ((a,a), (b,b), (c,c), (d,d)}
R-1 = {(a,a), (b,b), (c,c), (d,d)}
⇒ R = R-1.
Try these questions
-
If A = {12,13} B = {a,b}. Find A x B and show that n(A) * n(B) = n(A x B)
Answer
A x B = {(12,a), (12,b), (13,a), (13,b)}
n(A) = 2
n(B) = 2
n(A) ∗ n(B) = 2 ∗2 = 4
n (A x B) = 4
∴ n(A) ∗ n(B) = n(A x B)
-
If A = {2,4,6} B = {1,3,9}, R is defined as (x,y) ∉R 'x is greater than y'. Find R and (R-1)
Answer
R = {(2,1) (4,1)(4,3)(6,1)(6,3)}
R-1 = {(1,2) (1,4)(3,4)(1,6)(3,6)}
-
Write the domains and ranges of R and R-1 for the following relations.
R1 = {(1,2), (2,3), (3,4), (4,5)}
R2 = {(1,1), (2,4), (3,9), (4,16), (5,25)}
R3 = {(2,7), (3,8), (4,9), (5,10)}
Answer
-
Domain of R1= {1,2,3,4}
Range of R1 = {2,3,4,5}
R1-1 = {(2,1), (3,2), (4,3), (5,4)}
Domain of R1-1 = {2,3,4,5}
Range of R1-1 = {1,2,3,4}
-
Domain of R2= {1,2,3,4,5}
Range of R2= {1,4,9,16,25}
R2-1 = {(1,1), (4,2), (9,3), (16,4), (25,5)}
Domain of R2-1 = {1,4,9,16,25}
Range of R2-1 = {1,2,3,4,5}
-
Domain of R3= {2,3,4,5}
Range of R3= {7,8,9,10}
R3-1 = {(7,2), (8,3), (9,4), (10,5)}
Domain of R3-1 = {7,8,9,10}
Range of R3-1 = {2,3,4,5}