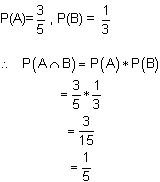An event is considered a subset of a sample space.
If we toss a die once the sample space is the set S = {1, 2, 3, 4, 5, 6} where each outcome is equally likely to happen.
If we want the event to be the number 3 on the die when it is tossed then the subset of the sample space is {3}.
It is a singleton set. Such an even this called a simple event.
If however we consider the event as 'getting a prime number' the subset of the sample space is {2, 3, 5} which has 3 elements.
Such an event is called a compound event.
If we toss a die, we can get an 'even number' or an 'odd number' but not both. So the event A of getting an even number excludes the event B of getting an odd number and vice versa. We call such events mutually exclusive events.
When we toss a coin, getting a head or getting a tail are mutually exclusive.
If we draw a card and our events are
A: getting a spade
B: getting a king
We can get the king of spades so these events are not mutually exclusive.
Dependent and Independent Event:
Suppose a bag contains 4 red balls and 8 black balls. Two balls are drawn one after the other without the first being replaced. Let A be the event of "getting a black ball in the first draw" and B be of "getting a red ball" in the 2nd draw. Suppose the event A occurs that is we get a black ball in the first draw then P (B) = 4/11 (4 red balls out of 12 – 1 = 11 balls).
If however A does not occur that is, instead of drawing a black ball, a red ball is drawn first, then P (B) = 3/11 (4 - 1 red balls out of 12 –1 = 11 balls)
Obviously P(B) depends on whether A occurs or not.
In such a case the events are called Dependent Events.
On the other hand, if we toss a coin twice and event A is ‘getting a head in the first toss' event B is ‘getting a tail in the second toss’, P (B) remains the same whether we get a head in the first toss or not. Such events are called Independent Events.
We know that the probability of getting a number 6 in the throw of a dice is 1/6. What is the probability of getting a number other than 6? The numbers are 1, 2, 3, 4 or 5 or 5 favorable outcomes.
Odds of an event
Sometimes we hear people say the 'Odds of a particular team winning are 3 to 1'.
Suppose we shuffle a deck of cards what are the odds that the first card we draw is an ace?
Since there are 4 aces we know that the probability of getting an ace is
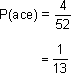
Probability of not getting an ace
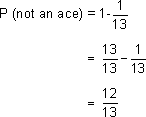
The probability of not drawing an ace is 12 times the probability of getting an ace. So the odds of getting an ace is 1 to 12 or the odds of not getting an ace is 12 to 1.
We can now form the following definition:
Suppose there are m outcomes favorable to an event and n outcomes which are unfavorable to the event in the sample space then
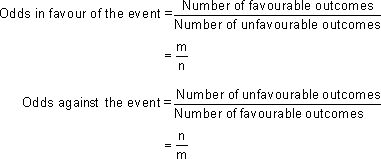
Example : 21
What are the odds in favor of getting a '4' in a throw of a die? What are the odds against getting a '4'
Solution:
Number of favorable outcomes = 1
Number of unfavorable outcomes = 6 - 1 = 5
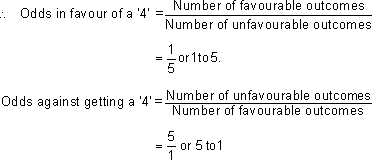
We can say that when we express odds in terms of probability then

Example : 22
The odds in favor of an event are 4 to 5. Find the probability that it will occur
Solution:
Odds in favor of the event occurring is 4/5. Thus

Probability that it will occur = 4/9.
Try these problems
If P(A) = 3/5 and P(B) = 1/3 find
a. P (A or B) if A and B are mutually exclusive events
b. P(A and B) if A and B are independent events
Answer:
- P(A) = 3/5 P(B) = 1/3
A and B are mutually exclusive events
P(A or B) = P(A ∪ B) = P(A) + P(B)
by the addition theorem of probability
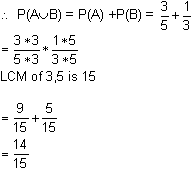
- A and B are independent events
 P(A and B) = P(A ∩ B) = P(A) * P(B)
By the addition theorem of probability
P(A and B) = P(A ∩ B) = P(A) * P(B)
By the addition theorem of probability