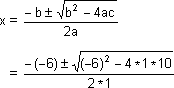Graphical Representation of Quadratic Expressions and Solutions to Quadratic Equations

You have learned how to solve simultaneous linear equations through graphs. We will now learn how to draw graphs of quadratic expressions in one valuable and, hence, solve to find the maxima, minima and zeros of the quadratic equation from the graph.

Consider these examples.

Example 1

Draw the graphs of the following functions.

1. f(x)=x²
2. f(x)=2x²

a.    Let y=f(x)=x²; we first obtain the points to be plotted

x	-3	-2	-1	0	1	2	3
x2	(-3)2	(-2)2	(-1)2	0	12	22	32
Y	9	4	1	0	1	4	9

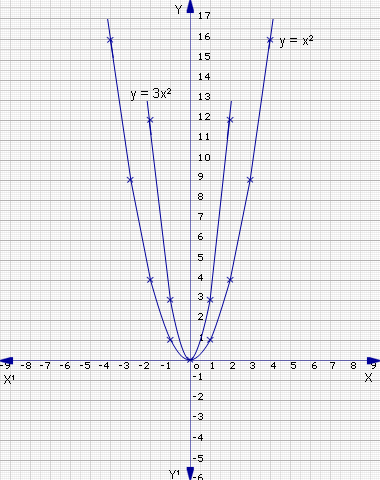
Plot the points (-3,9), (-2,4), (-1,1), (0,0), (1,1), (2,4), (3,9) and join them to form a smooth curve. The curve formed is called a parabola.

b.    Let y=f(x)=2x²

x	-3	-2	-1	0	1	2	3
x2	(-3)2	(-2)2	(-1)2	0	(1)2	(2)2	(3)2
2x2	29	24	21	0	21	24	29
y	18	8	2	0	2	8	18

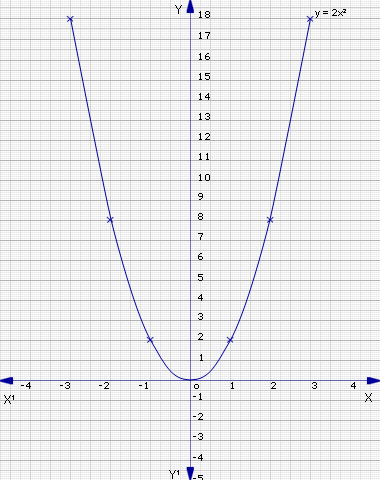
Plot the points (-3,18), (-2,8), (-1,2), (0,0), (1,2), (2,8), (3,18) and join them to form a smooth curve. Both graphs are parabolas.

As both pass through the point (0,0), they have common vertex. They also lie above the x-axis and are symmetric about the y-axis.

Example 2

Draw the 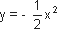graph of

x	-4	-2	0	2	4
x2	(-4)2	(-2)2	0	(2)2	(4)2
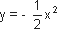
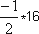
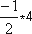
			0
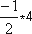
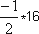
y	-8	-2	0	-2	-8

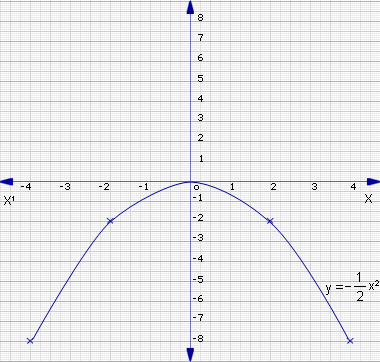
Plot the points (-4,-8). (-2,-2), (0,0), (2,-2), (4,-8) and join them to form a smooth curve.

Look at the graph of y = 1/2 x². It is also a parabola that lies below the x-axis in the third and fourth quadrants and is symmetrical about the y-axis.

Example 3

Draw the graph for y = 3x²

x	-2	-1	0	1	2
x2	(-2)2	(-1)2	0	(1)2	(2)2
3x2	34	31	0	31	34
y	12	3	0	3	12

Example 4

Draw the following curves and make a comparison.

1. f(y) = y²
2. f(y) = 2y²
3. f(y) = -1 / 3 y²
4. f(x) = -y²

a.    Let x = f(y) = y²

We can find the points to be plotted as follows.

y	-3	-2	-1	0	1	2	3
x2	(-3)2	(-2)2	(-1)2	0	12	22	32
x	9	4	1	0	1	4	9

However, when we plot the points, we take them in the form (x,y).

Plot the points (9,-3), (4,-2), (1,-1), (0,0), (1,1), (4,2), (9,3) and join them to form a smooth curve.

b.    Let x = f(y) = 2y²

y	-3	-2	-1	0	1	2	3
y2	(-3)2	(-2)2	(-1)2	0	12	22	32
2y2	2*9	2*4	2*1	0	2*1	2*4	2*9
x	18	8	2	0	2	8	18

Plot the points (18,-3), (8,-2), (2,-1), (0,0), (2,1), (8,2), (18,3) and join them to form a smooth curve.

c.    Let x = -1/3 y²

y	-6	-3	0	3	6
y2	(-6)2	(-3)2	0	32	62
-1/3y2	-1/3 * 36	-1/3 * 9	0	-1/3 * 9	-1/3 * 36
x	-12	-3	0	-3	-12

Plot the points (-12,-6), (-3,-3), (0,0), (-3,3), (-12,6) and join them to form a smooth curve.

d.    Let x=-y²

y	-3	-2	-1	0	1	2	3
-y2	-(-3)2	-(-2)2	-(-1)2	0	-(-1)2	-(-2)2	-(-3)2
x	-9	-4	-1	0	-1	-4	-9

Plot the points (-9,-3), (-4,-2), (-1,-1), (0,0), (-1,1), (-4,2), (-9,3) and join them to form a smooth curve.

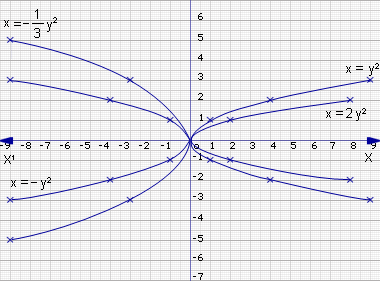
From the graphs, we find that the curves x = y², x = 2y² are parabolas symmetric about the x-axis and lie toward the right of the y-axis. They also lie in the first and fourth quadrants.

The curves x = -1/3 y², x = -y² are parabolas symmetric about the x-axis but lie to the left of the y-axis. They lie in the second and third quadrants.

Example 5

Draw the graph for f(x)=x²-x-12

Let y=x²-x-12

To plot the points, we find the value of y as follows.

f(-3)=(-3)²-(-3)-12

     =9+3-12

     =0

f(2) =(2)²-(2)-12

     =4-2-12

     =4-14

     =-10

In general, we use the following format.

y	-4	-3	-2	-1	0	1	2	3	4	5
x2	16	9	4	1	0	1	4	9	16	25
-x	+4	3	2	+1	0	-1	-2	-3	-4	-5
-12	-12	-12	-12	-12	-12	-12	-12	-12	-12	-12
y	8	0	-6	-10	-12	-12	-10	-6	0	8

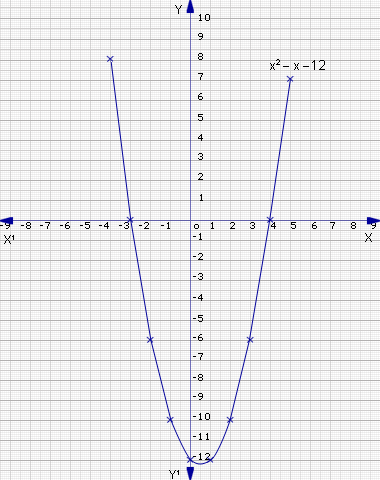
We plot the points (-4,8), (-3,0), (-2,6), (-1,-10), (0,-12), (1,-12), (2,-10), (3,6), (4,0), (5,8), and join them to form a smooth curve.

Observe that when y=0, x= -3 or 4 or y = 0 ⇒ x²-x-12=0

∴ the roots or solutions of x²-x-12=0 are x=-3, 4

Further, the curve cuts the x-axis at the points (-3,0) and (4,0). So the roots of the equation are the x-coordinates of the points, where the curve cuts the x-axis.

By looking at the graph, we can solve x²-x-12=0 by taking the points where the curve cuts the x-axis, i.e., (-3.0), (4,0).

We will now consider the graphs for equations of the form y=ax²+bx+c and see what happens when we change the coefficients of the x² and x terms, and the constant term.

First, we consider the quadratic equations of the form

y = ax²+b+c where the coefficient of x², which is a, changes.

Example 6

Draw the graphs of the following quadratic equations.

1. y = x²-3x-1
2. y = 2x²-3x-1
3. y = 3x²-3x-1
4. y = -x²-3x-1

i.    y = x²-3x-1

x	-2	-1	0	1	2	3	4
x2	4	1	0	1	4	9	16
-3x	+6	+3	0	-3	-6	-9	-12
-1	-1	-1	-1	-1	-1	-1	-1
y	9	3	-1	-3	-3	-1	-3

Plot the points (-2,9), (-1,3), (0,1), (1.-3), (2,-3), (3,-1), (4,3) and join them to form a smooth curve.

ii.    y = 2x²-3x-1

x	-1	0	1	2	3
x2	1	0	1	4	9
-2x2	2	0	2	8	18
-3x	3	0	-3	-6	-9
-1	-1	-1	-1	-1	-1
y	4	-1	-2	1	8

Plot the points (-1,4), (0,-1), (1,-2), (2,-1), (3,8) and join them to form a smooth curve.

iii.    y=3x²-3x-1

x	-1	0	1	2
x2	1	0	1	4
3x2	3	0	3	12
-3x	3	0	-3	-6
-1	-1	-1	-1	-1
y	5	-1	-1	5

Plot the points (-1,5), (0,-1), (1-1), (2,5) and join them to form a smooth curve.

iv.    y=-x2-3x-1

X	-4	-3	-2	-1	0	1	2
-x2	-16	-9	-4	-1	0	-1	-4
-3x	12	+9	+6	+3	0	-3	-6
-1	-1	-1	-1	-1	-1	-1	-1
Y	-5	-1	1	1	-1	-5	-11

Plot the points (-4,-5), (-3,-1), (-2,1), (-1,1), (0,-1), (1,-5), (2,-11) and join them to form a smooth curve.

The scale taken for the graph is

x-axis 1 unit = 2 cm

y-axis 1 unit = 1cm

On the x-axis, each decimal fraction is denoted by two divisions so that 0.2 = 2* 2 = 4 small divisions on the graph.

1.2 = 1.2*2 = 24 small divisions on the graph.

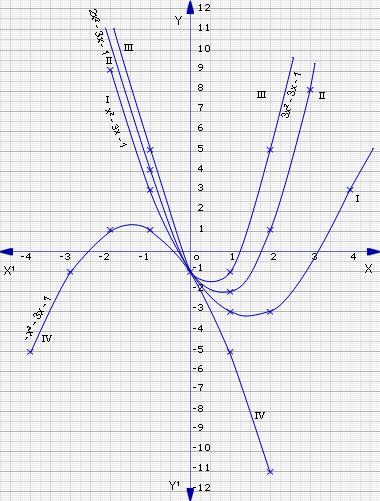
Comparing the graphs, we notice that the curves i, ii, iii, iv all meet at the point (0,-1)

All of the curves cross the x-axis so their roots are real.

Curve i: y = x²-3x-1 meets the x-axis at the points

(-0.3,0) and (3.3,0)

So the roots of x²-3x-1 = 0 are x = -0.3, 3.3

Curve ii: y = 2x²-3x-1 meets the x-axis at the points

(-0.3,0) and (1.7,0)

So the roots of 2x²-3x-1 = 0 are x = -0.3, 1.7

Observe that curves i and ii intersect

at (0,-1) and (-0.3,0)

Curve iii: y = 3x²-3x-1 meets the x-axis at (-0.2,0), (1.2,0)

So the roots of 3x²-3x-1 = 0 are x = -0.2, 1.2

Curve iv y = -x²-3x-1 meets the x-axis at the points

(-2.6,0) and (-0.4,0)

So the roots of the equation -x²-3x-1 = 0 are

x = -2.6, -0.4

Now consider the quadratic equations where

the coefficient of x, b, changes.

Example 7

Consider the following quadratic equations.

1. y = x²-5x+1
2. y = x²-3x+1
3. y = x²+2x+1
4. y = x^2+4x+1

i.    y = x²-5x+1

x	-2	-1	0	1	2	3	4
x2	4	1	0	1	4	9	16
-5x	+10	+5	0	-5	-10	-15	-20

+1	+1	+1	1	1	1	1	1
y	15	7	1	-3	-5	-5	-3

Plot the points (-2,15), (-1,7), (0,1), (1,-3), (2,-5), (3,-5), (4,-3) and join them to form a smooth curve.

ii.    y = x²-3x+1

x	-2	-1	0	1	2	3
x2	4	1	0	1	4	9
-3x	6	3	0	-3	-6	-9
1	1	1	1	1	1	1
y	11	5	1	-1	-1	1

Plot the points (-2,11), (-1,5), (0,1), (1,-1), (2,-1), (3,1) and join them to form a smooth curve.

iii.    y = x²+2x+1

x	-3	-2	-1	0	1	2
x2	9	4	1	0	1	4
2x	-6	-4	-2	0	2	4
+1	+1	1	1	1	1	1
y	4	1	0	1	4	9

Plot the points (-3,4), (-2,1), (-1,0), (0,1), (1,4), (2,9) and join them to form a smooth curve.

iv.    y = x²+4x+1

x	-4	-3	-2	-1	0	1
x2	16	9	4	1	0	1
4x	-16	-12	-8	-4	0	4
1	1	1	1	1	1	1
y	1	-2	-3	-2	1	6

Plot the points (-4,1), (-3,-2), (-2,-3), (-1,-2), (0,1), (1,6) Scale.

x-axis 1unit = 2 cm

y-axis 1unit = 1 cm

We can make the following observations.

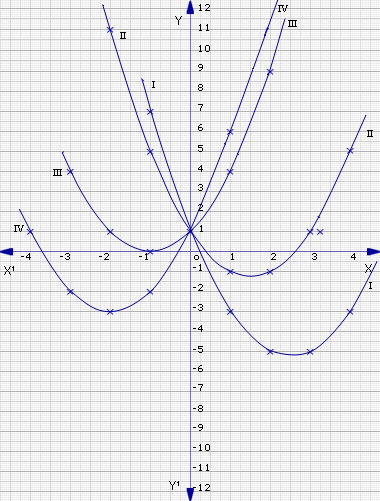
All pf the curves intersect at the point (0,1).

Curve i: y=x²-5x+1 meets the x-axis at the points

(0.2,0), and (4.8,0)

So the roots of x²-5x+1=0 are x=0.2, x=4.8

Curve ii: y=x²-3x+1 meets the x-axis at the points

(0.4,0) and (2.6,0)

So the roots of x²-3x+1=0 are x=0.4, 2.6

Curve iii: y=x²+2x+1 meets the x-axis at the point

(-1,0). So the roots are repeated

So roots of x²+2x+1=0 are x=-1, -1

Curve iv: y=x²+4x+1 meets the x-axis at (-3.7,0)

and (-0.3,0)

So roots of x²+4x+1=0 are x=-3.7, -0.3

We now consider the curve where the constant term c of ax²+bx+c varies.

Example 8

Consider the following quadratic equations.

1. y = x²+2x-3
2. y = x²+2x+2
3. y = x²+2x-6
4. y = x²+2x+4

i.    y = x²+2x-3

x	-4	-3	-2	-1	0	1	2	3
x2	16	9	4	1	0	1	4	9
2x	-8	-6	-4	-2	0	2	4	6
-3	-3	-3	-3	-3	-3	-3	-3	-3
y	5	0	-3	-4	-3	0	5	12

Plot the points (-4,5), (-3,0), (-2,-3), (-1,-4), (0,-3), (1,0), (2,5), (3,12) and join them to form a smooth curve.

ii.    y = x²+2x+2

x	-3	-2	-1	0	1	2	3
x2	9	4	1	0	1	4	9
2x	-6	-4	-2	0	2	4	6
2	2	2	2	2	2	2	2
y	5	2	1	2	5	10	17

Plot the point (-3,5), (-2,2), (-1,1), (0,2), (1,5), (2,10), (3,17) and join them to form a smooth curve.

iii.    y = x²+2x-6

x	-4	-3	-2	-1	0	1	2	3	4
x2	16	9	4	1	0	1	4	9	16
2x	-8	-6	-4	-2	0	2	4	6	8
-6	-6	-6	-6	-6	-6	-6	-6	-6	-6
y	2	-3	-6	-7	-6	-3	2	9	18

Plot the points (-4,2), (-3,-3), (-2,-6), (-1,-7), (0,-6), (1,-3), (2,2), (3,9), (4,18) and join them to form a smooth curve.

iv.    y = x²+2x+4

x	-2	-1	0	1	2
x2	4	1	0	1	4
2x	-4	-2	0	2	4
4	4	4	4	4	4
y	4	3	4	7	12

Plot the points (-2,4), (-1,3), (0,4), (1,7), (2,12) and join them to form a smooth curve.

The scale is the same as the previous two examples.

We observe that, none of the curves intersect.

Curve i: y²= x²+2x-3 intersects the x-axis at the points

(-3,0), and (1,0)

The roots of x²+2x-3 = 0 are therefore x = -3,1

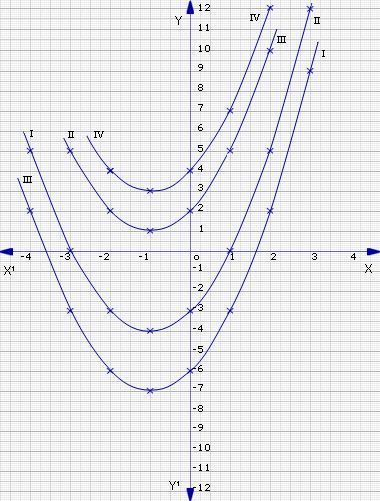
Curve iii: y = x²+2x-6 intersects the x-axis at the points

(-3.6,0) and (1.6,0)

So the roots of x²+2x-6 = 0 are x = -3.6, 1.6

Curves ii and iv: that is y = x2+2x+2 and y = x2+2x+4,

do not touch or cut the x-axis.

So the quadratic equations x²+2x+2 = 0 and x²+2x+4 = 0 have no real roots. Their roots are complex and are obtained algebraically by using the formula x²+2x+2 = 0

a = 1,    b = 2,    c = 2,

Discriminant = b2-4ac

    = (2)2 - 4*1*2

    = 4 - 8

    = -4 < 0

Using the formula

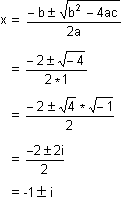
x = -1+ i, -1-i

x²+2x+4 = 0

a = 1,   b = 2,    c = 4

Discriminant Δ = b2-4ac

                          = (2)²-4*1*4

                          = 4-16

                          = -12 < 0

Using the formula

Using the formula

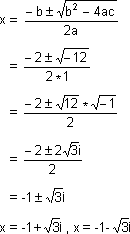
From the graph, how does one obtain the roots?

Consider Curve iii. The curve cuts the x-axis at a distance of 7.2 cm from 0 to its left.

Since each unit = 2 cm, we divide 7.2 by 2

7.2/2 = 3.6

∴ The point is 3.6 units along the x-axis, which is the point (-3.6,0)

The curve also cuts the x-axis at a distance of 3.2 cm from 0 to its right.

We therefore obtain 3.2/2 = 1.6 units.

So the point is actually (1.6, 0)

Example 9

Consider the following quadratic equations.

Draw the graphs of:

1. y = 2x²+x-1
2. y = x²-6x+9
3. y = x²-4x+5

i.    y = 2x2+x-1

x	-3	-2	-1	0	1	2
x2	9	4	1	0	1	4
2x2	18	8	2	0	2	8
x	-3	-2	-1	0	1	2
-1	-1	-1	-1	-1	-1	-1
y	14	5	0	-1	2	9

Plot the points (-3,14), (2,5), (-1,0), (0,-1), (1,2), (2,9) and join them to form a smooth curve.

ii.    y = x2-6x+9

x	-1	0	1	2	3	4
x2	1	0	1	4	9	16
-6x	+6	0	-6	-12	-18	-24
9	9	9	9	9	9	9
y	16	9	4	+1	0	1

Plot the points (-1,16), (0,9), (1,4), (2,1), (3,0), (4,1) and join them to form a smooth curve.

iii.    y = x²-4x+5

x	-2	-1	0	1	2	3
x2	4	1	0	1	4	9
-4x	8	4	0	-4	-8	-12
5	5	5	5	5	5	5
y	17	10	5	2	1	2

Plot the points (-2,17), (-1,10), (0,5), (1,2), (2,1) and (3,2) and join them to form a smooth curve.

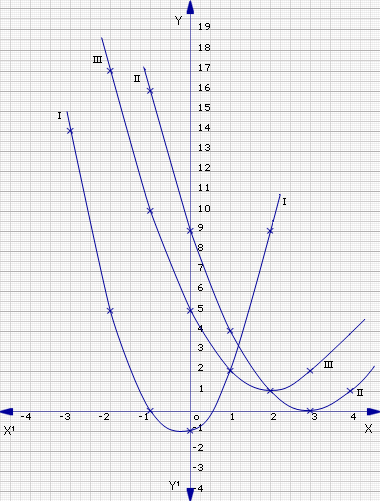
Curve i: y=2x²+x-1 cuts the x-axis at two points (-1,0) and (+1 / 2), 0.

So 2x²+x-1=0 has 2 real roots x = 1, +1/2

Curve ii: y = x²-6x+9 touches the x-axis at the point (3,0).

The equation x²-6x+9 = 0 has two equal roots, or repeated roots, which are x = 3, 3.

Curve iii: y = x2-4x+5 does not touch or cut the x-axis at all. This means that x2-4x+5 = 0 has no real roots, but has only complex roots. These roots have to be obtained algebraically.

x²-4x+5=0

a = 1,    b = -4,    c = 5.

Discriminant Δ = b2-4ac

     = (-4)² - 4*1*5

     = 16 - 20

     = -4 < 0

Using the formula, we get the roots as follows.

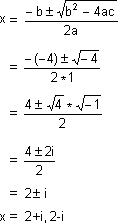
From this example, we infer the following about the roots of the equation.

ax²+bx+c = 0 a≠ 0. a, b, c are real numbers -------(1)

1. If the curve y = ax²+bx+c meets the x-axis at two points (x1,0), (x2,0) then x1, x2 are two distinct real roots of equation (1)
2. If the curve y = ax²+bx+c meets the x-axis in exactly one point (x1,0), equation (1) has exactly one root, which is a coincident or repeated root.
3. If the curve y = ax²+bx+c never meets the x-axis, then its roots are complex numbers.

There is another way to obtain the roots of the equation.

ax²+bx+c = 0 --------(1)

This can be rewritten as

ax² = -bx-c ---------(2)

Let y = ax2 ---------(3)

and y = -bx-c ---------(4)

Equation (3) forms a parabola.

Equation (4) is a straight line.

We next draw the graphs to the same scale.

1. If in the graph, (4) cuts (3); that is, the straight line cuts the curve in two points so that their x-coordinates are the same. Then (1) has two real roots.
2. If the line and the curve have a single point in common, then their x-coordinate is the only root of equation (1); that is, the root is repeated.
3. If the line and the curve have no points in common, then equation (1) has only complex roots.

The following example will illustrate these points.

Example 10

Solve graphically

x²+2x-15 = 0

This can be rewritten as

x² = -2x+15

Let y = x²

and y = -2x-15

y = x²

x	-3	-2	-1	0	1	2	3
x2	9	4	1	0	1	4	9
4y	9	4	1	0	1	4	9

Plot the points (-3,9), (-2,4), (-1,1), (0,0), (1,1), (2,4), (3,9) and join them to form a smooth curve.

Y = -2x+15

x	-5	-4	-3	-2	-1	0	1	2	3
-2x	10	8	6	4	2	0	-2	-4	-6
15	15	15	15	15	15	15	15	15	15
y	25	23	21	19	17	15	13	11	9

Plot the points and join them (-5,25), (-4,23), (-3,21), (-2,19), (-1,17), (0,15), (1,13), (2,11), (3,9).

From the graph, y = -2x+15 meets y = x² at the points (-5,25) and (3,9) since the x-coordinates represent the roots of the equation.

The roots of x²+2x-15=0 are x=-5, 3

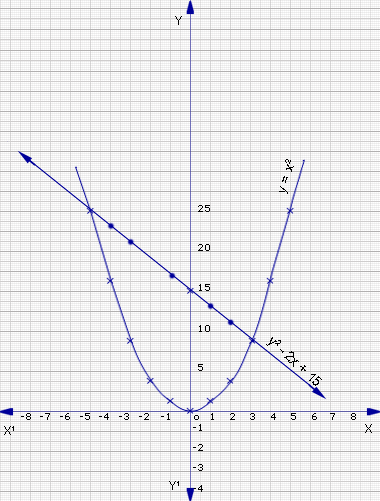
Try these questions

Solve graphically

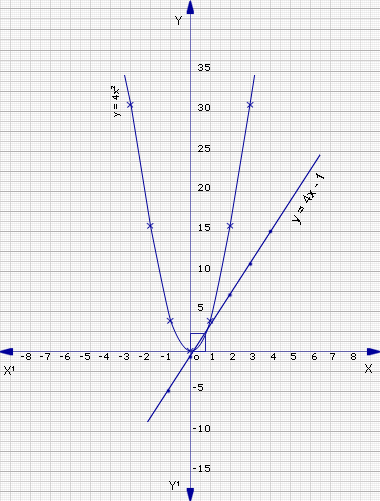
1. 4x² - 4x+1 = 0
   This can be rewritten as
   4x²=4x-1
   Let  y = 4x²
   and y = 4x-1
         y = 4x²

   X	-3	-2	-1	0	1	2	3
   x2	9	4	1	0	1	4	9
   4x2	36	16	4	0	4	16	36
   Y	36	16	4	0	4	16	36

   
   Plot the points (-3,36), (-2,16), (-1,4), (0,0), (1,4), (2,16), (3,36) and join them the form a smooth curve.
   y = 4x-1
   

   x	-1	4
   4x	-4	16
   -1	-1	-1
   y	-5	15

   
   Plot the points (-1,-5), (4,15) and join them to form a line.
   From the graph, the curve and line meet at exactly one point, (1/2,1).
   So the roots of 4x²-4x+1=0 are repeated.
   
   
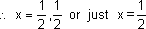
2. x²-6x+10 = 0
   This can be rewritten as
   x² = 6x-10
   Let y = x²
   and y = 6x-10
   y = x²
   

   x	-5	-4	-3	-2	-1	0	1	2	3	4	5
   x2	25	16	9	4	1	0	1	4	9	16	25
   y	25	16	9	4	1	0	1	4	9	16	25

   
   Plot the points (-5,25), (-4,16), (-3,9), (-2,4), (-1,1), (0,0), (1,1), (2,4), (3,9), (4,16), (5,25) and join them to form a smooth curve.
   

   x	0	2	3
   6x	0	12	18
   -10	-10	-10	-10
   y	-10	2	8

   
   Plot the points (0,-10), (2,2), (3,8) and join them to from a straight line.
   Since the line and curve do not intersect, the roots are complex.
   
   Solving algebraically x²-6x+10 = 0
   a =1,    b = -6,    c = 10