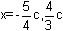Quadratic Equations - Solutions by Completing the Square Method

Consider the following identities

x²+2ax+a²=(x+a)²

x²-2ax+a²=(x-a)²

These trinomials are perfect squares. The highest power x² has unity (i.e., 1) as its coefficient. In this case, the term without an x (the constant term) must equal the square of half the coefficient of x. Therefore, if the terms x² and x are given, the square may be completed by adding the square of half the coefficient of x.

If ax²+bx+c=0

Transposing ax²+bx=-c

Dividing by a to make the coefficient of x² = 1 we get

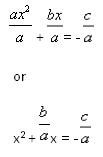
To complete the square, we add the square of half the coefficient of x, or

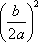   =         , to both sides of the equation

We obtain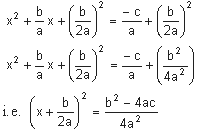      

Taking the square roots on both sides

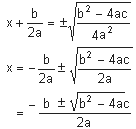
which is, as you know, the formula.

Example 1

Solve using the completing the square method

x²+14x=32

a=1, b=14, c= -32

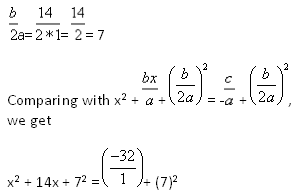
(x + 7)² = 32 + 49

(x + 7)² = 81

x + 7 = ± 9

i.e., x = 9 - 7 or x = -9 - 7

x = 2 or x = -16

Example 2

Solve the equation x²-2x=8 by completing the square,

comparing x² - 2x = 8 with x²+ b / a x = c / -a

a = 1, b = -2, c = -8

               x² - 2x + (1)² = 8 + (1)²

               (x - 1)² = 8 + 1

               (x - 1)² = 9

Taking square roots on both the sides

               x² - 1 = ± 3

x-1=3 or x-1=-3

x=1+3 or x=-3+1

x=4 or x=-2

Example 3

Solve by completing the square

       3x²-5x= 2

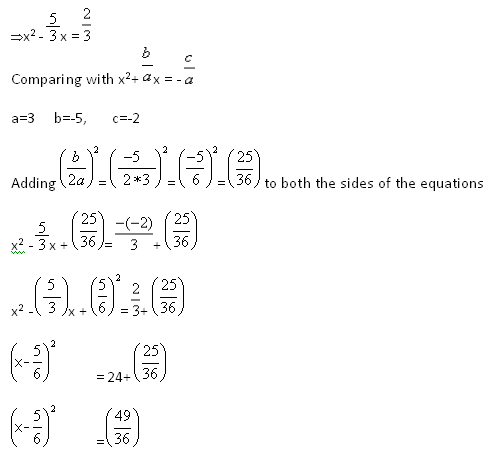
Taking the square roots on both sides

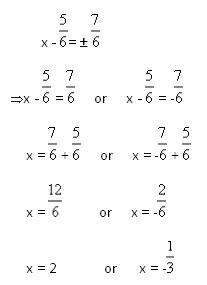
Try these questions:

Solve by completing the square

1. (2x-3) (3x+4) = 0

2. 3x²+7x = 6

3. 4x²-2x = 3

4. x² = 0.6x - 0.05

5. 5(x+2) = 4(2x-1)(x+1)-16

6. 2x²-7x = 4

7. 12x²-cx-20c2 = 0

Answers to Practice Problems

Solutions: To solve by completing the square.

1. (2x-3) (3x+4) = 0

   
   

   On expanding we get

   2x(3x+4) -3 (3x+4) = 0

          6x² +8x -9x -12 = 0

             6x²-x-12 = 0

   ⇒        6x²-x = 12

   
   

   Dividing throughout by 6 we get

   x² - x / 6= 12/6

   x² - x / 6 = 2        (1)

   Comparing with x² b / -a x = c / -a we get

   a=6 b= -1, c= -2

   

   




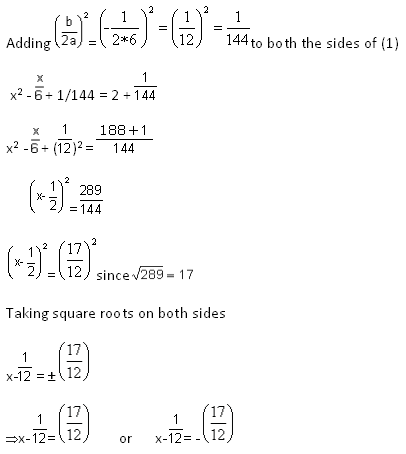
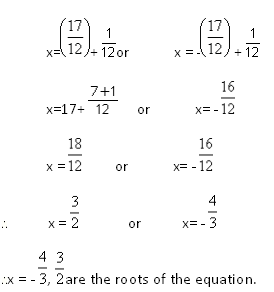
2. To solve 3x² + 7x = 6 by completing the square

   Dividing throughout by 3 we get

   

   

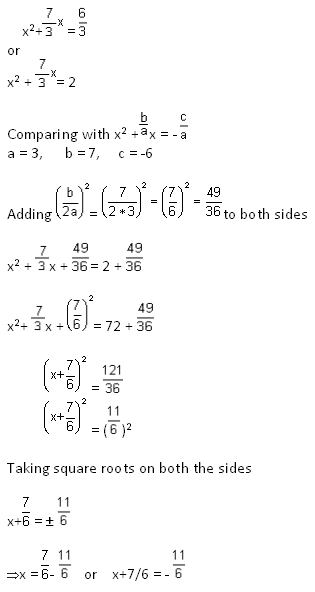
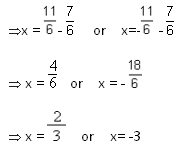
   ∴ x = 2/3, -3 are the roots of the equation.




3. To solve 4x²-2x = 3 by completing the square

   Dividing throughout by a = 4 we get

   x² 2 / -4 x = 3/4

   Comparing with x²+ b/a x= c/-a

   a=4 b=-2, c=-3

   

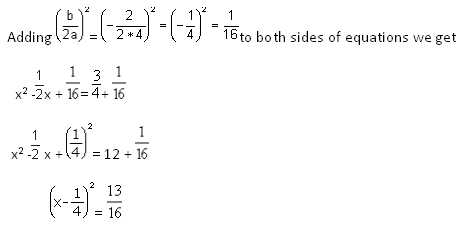
   Taking square roots on both the sides we get

   




4. To solve by completing the square

          x² = 0.6x - 0.05

   Transposing

          x²-0.6x = -0.05

   Comparing with x²+b / a x = c / -a

   a = 1, b = - 0.6, c = - 0.05

   
   

   Adding (b / 2a)² = (-0.6/2)² = (-0.3)² = .09 to both sides we get

   x²-0.6x+0.09 = -0.05+0.09

   x²-0.6x+(0.3)² = 0.04

          (x-0.3)² = (0.2)²

   Taking square roots on both the sides

   x - 0.3 = ± 0.2

   ⇒ x-0.3 = 0.2 or x - 0.3 = - 0.2

   ⇒        x = 0.2 + 0.3 or x = - 0.2 + 0.3

   ⇒        x = 0.5 or x = 0.1

   Roots of the equations are x = 0.1, 0.5




5. To solve 5(x+2) = 4(2x-1)(x+1) -16 by completing the square

   We first obtain the form ax² + bx + c = 0

   5x+10 = 4[(2x -1)x+(2x - 1) * 1] -16

   5x+10 = 4[2x²-x+2x-1]-16

   5x+10 = 4[2x² + x - 1] -16

   5x+10 = 8x² + 4x - 4 - 16

   ⇒ 8x² + 4x - 20 - 5x - 10 = 0

   ⇒        8x² - x - 30 = 0

   ⇒        8x² - x = 30

   Dividing throughout by 8

   

   




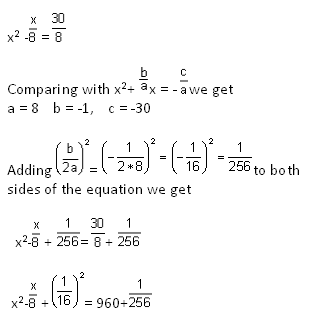
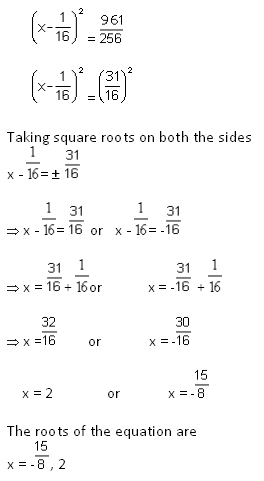
6. To solve 2x²-7x = 4 by completing the square

   Dividing throughout by a = 2

   

   




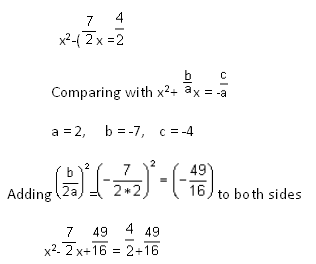
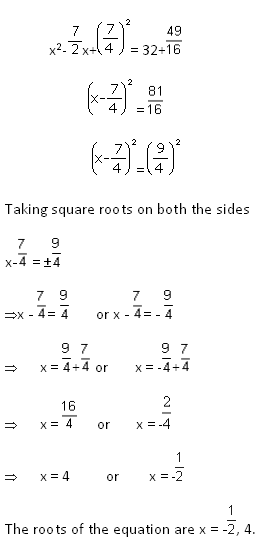
7. To solve 12x²-cx-20c2 = 0 by completing the square Transposing and dividing by a = 12 we get

   x²c / -12 x = 20 / 12 c2

   Comparing with x + (b/-a) x = -c/a

   a = 12, b = -c, c = - 20c2

   
   

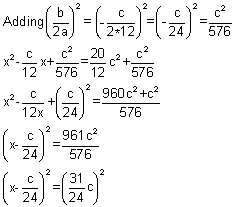       to both sides

   Taking square roots on both sides

   

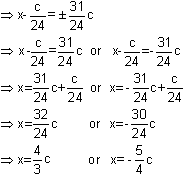
   Roots of the equations are