Let’s imagine that we need to select any two letters from the three letters a, b, c. We can select them in three different ways.
ab, ac, bc
Selection of these objects in this way is known as a combination.
Now say that we have three objects a, b, c in a hat and we have to select any two of them.
We can first choose a then b or first b then a and so on. . .
All together, we can choose two of them in six different ways.
ab, ba, ac, ca, ba, ca
This arrangement is called a permutation.
Fundamental principle of counting
Before we go into detail about permutations and combinations, let’s first talk about the fundamental principle of counting.
Suppose something can be selected in m different ways, after which something else can be selected in n ways. Then the number of ways both can be selected is m*n.
Imagine that you have a, b, c, d in a basket and you have to pick two of them in succession. We can draw the first one in one of four ways; that is, either you can pick a or b or c or d.
Once you select the first one, you have only three options left when selecting the second one.
Therefore, you have 4 ∗3 = 12 possible ways to choose two letters from the four.
ab ba ca da
ac bc cb db
ad bd cd dc
ab means that a was taken first and then b; ba means that b was taken first and then a, and so on.
Defining permutations
Linear Permutations
From the elements of a finite set “A”, taking some or all the elements and arranging them linearly is called a linear permutation.
Similar Permutations
If in a given set of objects some objects are alike, then permutations formed from them are known as similar permutations. In this case, the number of permutations will change because we cannot identify the change among the like objects.
Circular Permutations
If “n” distinct objects are arranged in a circular manner, givinG.P. reference only to relative positions, then we call this a circular permutation.
In a circular permutation, if the places are changed circularly, the permutations will not change.
Example
If A = {4, 5, 6} then the permutations obtained by arranging all elements in A in order are 456, 465, 546, 564, 645, 654.
Notation
The product of the first “n” natural numbers is called n factorial and is denoted by n! We denote 0! = 1 and we observe that 1! = 1.
For example: 6! = 6 ∗5 ∗4 ∗3 ∗2 ∗1 = 720.
From a set A of n elements, the number of permutations taken r (where r ≤n) at a time is denoted by npr or p(n , r).
Theorem
The number of permutations of n dissimilar things taken
r (where r ≤ n) at a time is npr = n(n – 1)(n – 2), . . . (n – r = 1).
Proof
Let A be a set of n dissimilar things. Note that the number of permutations taken r at a time from the set A of n dissimilar things is equal to the number of selections of r distinct objects taken one after the other.
Let us make A1 = A, n(A1) = n(A) = n. After selection for the first place is made, let A2 be the set of selections for the second place.
Then A2⊆ A and
n(A1) – 1 = n – 1.
Repeating the above argument, we have A3 ⊆ A2 and
n(A3) = n(A2) – 1 = n – 1 – 1 = n – 2 = n – (3 – 1).
Based on the same argument, if Ar is the set of selections for the rth place, then it follows that
n(Ar) = n – (r – 1) = n – r + 1.
Now, from the fundamental principle
npr = n(A1) n(A2), . . . n(Ar)
= n(n – 1)(n – 2), . . . n(n – r + 1).
A finite bijective mapping is a permutation.
If S = {a, b, c, d, e} and defining a permutation
f(a) = b; f(b) = d; f(c )= a; f(d) = e; f(e) = c; then we denote the permutation f as
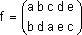
npn = n(n – 1)(n – 2), . . . (n – n + 1)
= n(n – 1)(n – 2), . . . 2.1
= 1 * 2 * 3, . . . (n – 2)(n – 1) n = n!.
That is, the number of permutations containing all objects from “n” distinct things is npn = n!
npr = n(n – 1)(n – 2), . . . (n – r + 1)
n(n – 1)(n – 2), . . . (n – r + 1)[(n – r )!]
= —————————————————
(n – r)!
1 * 2 * 3, . . . (n – 1) * n
= ———————————
(n – r)!
npr = n!/(n – r)!
Examples
- What is the value of 8! / 4! ? Is 8! / 4! = 2! True?
Solution:
8 * 7 * 6 * 5 * 4 * 3 * 2 *1
8! / 4! = ————————————
4 * 3 * 2 * 1
= 8 * 7 * 6 * 5 = 1680.
But 2! = 2 *1 = 2
∴ 8! / 2! ≠ 2!.
- Show that (2n)! = 2n (n!) [1 *3 *5, . . . (2n – 1)]
Solution:
(2n)! = (2n)(2n – 1)(2n – 2), . . . 3 * 2*1
= [(2n)(2n – 2)(2n – 4), . . .4 *2] * [(2n – 1)(2n – 3), . . .3 *1]
= [(2)(n)(2)(n – 1)(2)(n – 2), . . . 2 *1] *[1 *3 *5, . . . (2n – 1)]
= (2 * 2, . . .2) [n(n – 1)(n – 2), . .. 2 *1)] * [1 * 3 * 5, . .(2n – 1)]
(n times)
= 2n * n! [1 * 3 * 5, . . . (2n – 1)]
Try these questions
- If np5 = 42 np3 (n > 4) then what is the value of n ?
Solution:
Given that np5 = 42 np3
n! 42 n!
——— = ———
(n – 5)! (n – 3)!
(n – 3)!
⇒ ——— = 42
(n – 5)!
⇒ (n – 3)(n – 4) = 42
⇒ n2 – 7n + 12 = 42
⇒ n2 – 7n – 30 = 0
⇒ (n – 10)(n + 3) = 0
⇒ n = 10 or n = -3
But n is a positive integer and greater than 4.
∴ n = 10
- If the letters in the word REALMS are arranged in all possible ways in dictionary order and without repetition, what is the rank of the given word?
Solution:
The alphabetical order of the letters of the given word
REALMS is A, E, L, M, R, S.
∴ The number of words that begin with A is 5! = 120
Similarly,
The number of words that begin with E is 5! = 120
The number of words that begin with L is 5! = 120
The number of words that begin with M is 5! = 120
The number of words that begin with ‘RA’ is 4! = 24
Therefore, per the dictionary the next word is REALMS.
So the number of words that come before the word
REALMS = 120 + 120 + 120 + 120 + 24 = 504.
∴ REALMS is the 505th word.
Theorem
npr = (n-1)pr + r* (n-1)p (r-1)
Proof
By selecting “r” objects from “n” distinct objects, the number of permutations npr can be split in to two types. Those are
- permutations having a particular object.
- permutations without that object.
- Find the number of permutations having a particular object.
Keep that object in any one of the “r” vacancies. This can be done in “r” ways. The remaining (r – 1) vacancies can be filled by
(n – 1) objects in (n-1)p (r-1)ways.
Since these two things are independent, the number of permutations with a particular object is r*(n-1)p (r-1)
To find the number of permutations without having a particular object.
First, we have to remove that particular object. From the remaining (n – 1) objects, r objects can be selected and arranged in (n-1)p r ways,
∴ The required number of permutations
= npr = (n-1)pr + r * (n-1)p (r-1)