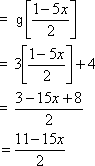Consider three non-empty sets, as drawn below.
Let f be a function from A into B and g be a function from B into C. For any a ∈ A, there exists an f (a) ∈ B.
If we take B as the domain of g, then for any f (a) ∈ B, there exists a g[f(a)] ∈ C. So g[f(a)] is defined.
We now have a rule that for every a ∈ A, the rule assigns a to a unique g[f(a)] in C. So we have a new function from A into C. This function is called the composite function of f and g and is denoted by g o f [read as “g circle f”].
Definition
Let f: A→B, g : B →C be two functions. Then the composite function of f and g denoted by gof is gof: A→C and is defined by (gof)(x) = g[ f (x)].
The composite function is also called the product function.
Notice that
- The codomain of f is the domain of g.
- The domain of gof is the domain of f.
- The codomain of gof is the codomain of g.
Example 1
Let f: A→B, g : B →C be defined as given below.
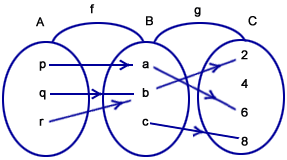
gof(p) = g[f(p)] = g(a) = 6
gof(q) = g[f(q)] = g(b) = 2
gof(r) = g[f(r)] = g(b) = 2
Example 2
Let f = {(1,2), (2,3), (3,4)} g = {(2,1), (3,2), (4,4)}. Find gof.
gof(1) = g[f(1)] = g(2) = 1
gof(2) = g[f(2)] = g(3) = 2
gof(3) = g[f(3)] = g(4) = 4
 gof = { (1,1), (2,2), (3,4)}
gof = { (1,1), (2,2), (3,4)}
Can we find fog ?
(fog)(x) = f(g(x))
f(g(2)) = f(1) = 2
f(g(3)) = f(2) = 1
f(g(4)) = f(4) which is undefined.
So fog is not defined.
Example 3
Let f: R→R, g:R→R defined by f(x) = 3x-2 g(x) = x - 2/3. Find gof and fog.
Both gof and fog are defined.
(fog)(x) = f[g(x)] = f(x-2/3]
= 3(x - 2/3) - 2
= 3x - 3*2/3 - 2
= 3x-4
(gof)(x) = g[f(x)] = g[3x-2]
= 3x-2-2/3
= 3x - (6+2/3)
= 3x - 8/3
We can see that
fog ≠ gof.
Example 4
Let f(x) = x-2 g(x) = x2+1 where f:R→R and g:R→R.
Find i) gof(-4), ii) (fog)(-4), iii) Give rules for fog and gof.
Solutions:
i) gof (-4)
= g[f(-4)]
= g[-4-2]
= g(-6)
= (-6)2+1
= 36+1
= 37
ii) fog(-4) = f[g(-4)]
= f[(-4)2 + 1]
= f[16+1]
= f(17)
= 17-2
= 15
iii) fog(x) = f[g(x)] = f(x2+1)
= (x2+1) - 2
= x2+1-2
= x2-1
gof = g[f(x)] = g[x-2]
= (x-2)2 + 1
= x2 - 4x + 2 + 1
= x2 - 4x + 3
= x2 - 4x + 2 + 1
= x2 - 4x + 3
Consider the following figure.
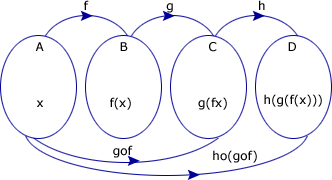
Let f: A→B, g: B→C, h: C→D
We can obtain the composite function
gof: A→C
h : C→D
We can combine them to get the function h[gof(x)] = (hogof)(x) or hogof(x) = h[g(f(x))]
Now consider this figure.
- both have the same domain A
- both have the same codomain D
- for every x ∈A, there exists the same image h[g(f(x))] in D.
Example 5
Let f: R→R, g: R→R, h: R→R. If f(x) = x2+2, g(x) = 3x-1, h(x) = 1-x2.
Find a) ho(gof)(-5) b) (hog)of (-5) c) rules for ho(gof).
-
ho(gof)(-5) = ho[g(f (-5)]
= ho[g((-5)2+2)]
= ho[g(25+2)]
= ho[g(27)]
= ho[3*27-1]
= ho[81-1]
= h ((80))
= 1 - (80)2
= 1 - 6400
= - 6399.
-
(hog)of (-5) = (hog)[f(-5)]
= (hog)[(-5)2+2]
= (hog)[27]
= h[g(27)]
= h[3 *27-1]
= h[81-1]
= h(80)
= 1 - (80)2
= 1- 6400
= - 6399
-
ho(gof) (x) = ho[g(f(x))]
= ho[g(x2+2)]
= h[3(x2+2)-1]
= h[3x2+6-1]
= h[3x2+5]
= 1-(3x2+5)2
= 1-(9x4+30x2+25)
= 1-9x4-30x2-25
= -9x4-30x2-24
Try these questions:
-
Let A = {2,4,6,8} B = {1,2,3,4} C = {11,12,13}. Let f: A→B, g: B→C be defined as
f = {(2,2), (4,1), (6,4), (8,3)} g = {(1,11), {2,12), (3,13), (4,11)} Find gof.
Solution:
A = {2,4,6,8} B = {1,2,3,4} C = {11,12,13}.
f = {(2,2), (4,1), (6,4), (8,3)}
g = {(1,11), {2,12), (3,13), (4,11)}
To find gof
gof(2) = g[f(2)]
= g(2) = 12
gof(4) = g[f(4)]
= g[1]
= 11
gof(6) = g[f(6)]
= g(4)
= 11
gof(8) = g[f(8)]
= g(3)
= 13
gof = { (2,12), (4,11), (6,11), (8,13)}
- Let f: R→R and g: R→R be defined by f(x) = 1-5x / 2 g(x) = 3x+4. Find
a. fog(4)
b. gof(4)
c. fog(x)
d. gof(x)
Solutions:
f: R →R g : R →R defined by f(x) = 1- 5x / 2, g (x) = x/3x + 4
a. fog(4) = f[g(4)]
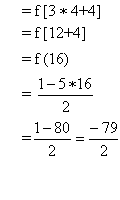
b. gof(4) = g[f(4)]
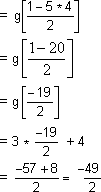
c. fog(x) = f[g(x)]
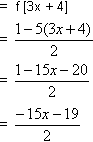
d. gof(x) = g[f(x)]