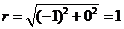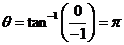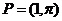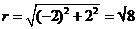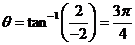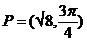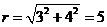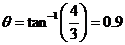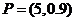Like the rectangular coordinate system, the polar coordinate system is used to represent data graphically. This
coordinate system is specified in terms of some point, called a pole, and some ray with a vertex at the pole, called a
polar axis. The pole is usually chosen to be where the point (0,0) would be in the rectangular coordinate system, and the
polar axis is usually co-incident with the positive x-axis.
The coordinate system itself (without data) is divided by radial lines (in units or Y) and concentric circles (in units of θ).
Although the X- and Y-axes are often drawn or printed in a polar coordinate system, this is typically only for reference
and clarity.
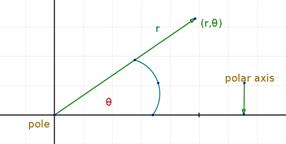
In the polar coordinate system, a point is specified by an ordered pair (r,θ ), called polar coordinates, where r is the
point's radial distance from the pole, and θ is the point's angular distancefrom the polar axis, measuring counterclockwise.
Examples Explanation
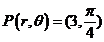
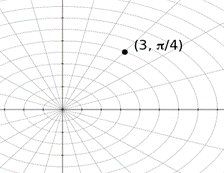
Converting Between Polar and Rectangular Coordinates
A point P with polar coordinates (r, θ) has rectangular coordinates (x,y) given by
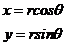
Examples Explanation
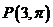
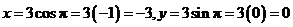
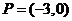
Converting from Rectangular to Polar Coordinates
A point P with rectangular coordinates (x,Y), has polar coordinates (r,θ) given by
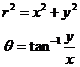
As the inverse tangent function can have multiple solutions, it is important to note the quadrant in which the point lies. In
the following example, the point (-1,1) lies in the fourth quadrant, and so θ must lie in that quadrant as well, even
though there is a solution to the equation for θ in the third quadrant.
Examples Explanation
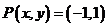
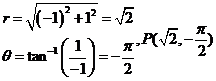
Try these exercises
Instructions
Graph
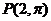
Graph
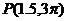
Graph
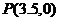
Where in the coordinate system is any point having r=0, regardless of the value of θ?
Express Q=(4,0) in rectangular coordinates.
Express P=(2,-π) in rectangular coordinates.
Express Q=(0,0) and P=(0,π) in rectangular coordinates. What is remarkable about the rectangular
coordinates of these two points?
Express P=(-1,0) in polar coordinates.
Express P=(-2,2) in polar coordinates.
Express P=(3,4) in polar coordinates. Round decimals to the nearest tenth.
Answers to questions:
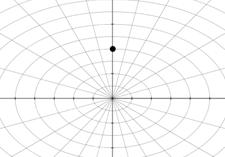
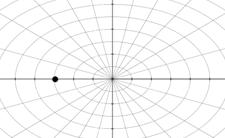

All points (0,θ) are at the pole (origin).
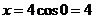
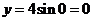
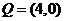
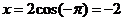
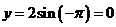
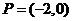
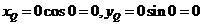
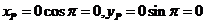
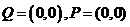
Both points have the same representation in rectangular coordinates.