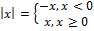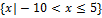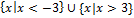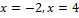A function that is defined by two or more different subfunctions is piecewise-defined. Each subfunction applies on its own portion of the piecewise-defined function’s domain (or, its own subdomain).

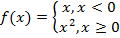
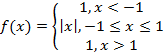
Evaluating Piecewise-Defined Functions

In order to evaluate a piecewise-defined function at a particular point, it is necessary to determine which of the function’s subdomains contains the point.

Rules

Examples

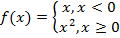
Find f(-3) and (0)

Explanation

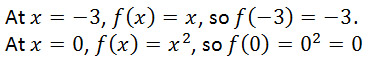
As in the last example, it is important to be careful when reading the subdomain of each subfunction in the function. Both subdomains contain 0, but only the domain of x²  includes 0. This is usually a matter of taking note of whether the domain is expressed with <,>  or  ≤,≥.

Domain of Piecewise-Defined Functions

The domain of a piecewise-defined function is a combination of its subfunctions’ individual subdomains.

Examples

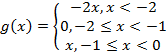
Explanation

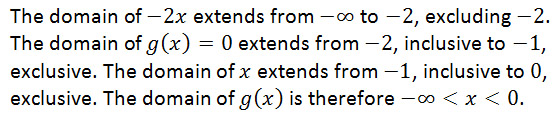
If there are one or more points in one or more subdomains at which the function is not defined, the function is said to be discontinuous at those points.

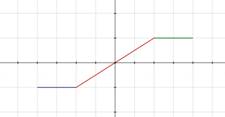
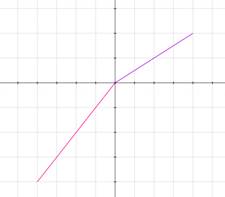
Graphing Piecewise-Defined Functions

Graphing these functions is a matter of graphing each component subfunction on its subdomain.

Examples

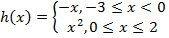
Explanation

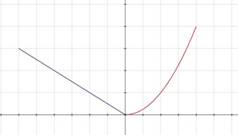
Try these exercises:

Instructions

1. 
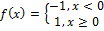
   Evaluate f(0)


2. 
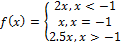
   Find f(-1)


3. 
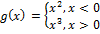
   Find f(0)


4. The absolute value function
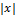   is a piecewise-defined function. Express it in function notation.


5. 
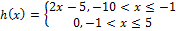
   Find the domain of h(x).


6. 
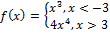
   Find the domain of f(x).


7. 
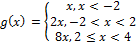
   Find the points at which g(x) is discontinuous.


8. Graph
   


9. Graph
   


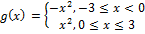
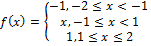
10. Graph
    

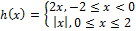
Answers to questions

1. 


2. 


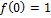
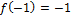
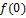3. is undefined.


4. 


5. 


6. 


7. 


8. 


9. 


10.