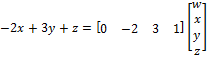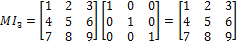Scalar Multiplication

In contrast to a matrix, which is a collection of values, a scalar is a single constant. To multiply a matrix by a scalar, simply find the product of the scalar and each matrix element individually.

Examples

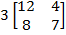
Explanation

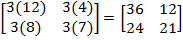
Matrix Products

A matrix product is the result of multiplying a row matrix and a column matrix. By definition, the row matrix must be the first operand. Corresponding entries are multiplied together (the first entry in the row times the first entry in the column, etc.), then the products are summed.

Examples

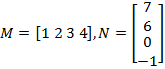
Explanation

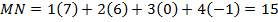
The row and column matrices must have the same number of elements to form a matrix product.

Matrix Multiplication

Matrices other than row and column matrices can also be multiplied. The order in which the multiplication is carried out is very important; matrix multiplication is not commutative (for matrices A,B AB ≠ BA ).

For matrices A,B, each entry a_ij of their product (the solution matrix AB) is the matrix product of the i th row of A and the j th column of B. Similar to the requirement for row and column matrices in a matrix product, the rows of A and the columns of B must have the same number of entries. Because the number of elements in a row is equal to the number of columns, and vice versa, this means that the number of columns of A (the first operand) must equal the number of rows of B.

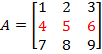
The rows of the matrix A each have 3 elements because A has 3 columns.

It is easy to check that this is true when we write the two dimensions side by side; the two “inner” values must be the same. If this is not the case, the matrices cannot be multiplied. The solution matrix will always have the same number of rows as the first matrix and the same number of columns as the second matrix (the “outer” values). In other words, an m*n matrix times an n*p will have dimension m*p.

Examples

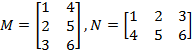
Explanation

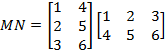
1. Determine if the matrices have the dimensions required for multiplication.
   M is 3*2 and N is 2*3. Putting these side by side, we see 3*22*3, and the middle numbers (2’s) are the same, so we can multiply MN.


2. Determine the size of the solution matrix.
   The size of the solution matrix consists of the two “outer” dimensions when the two dimensions are written side by side:3*22*3. So, the solution matrix will be 3*3


3. The element a _1,1 in the solution matrix is the matrix product of the first row of M and the first column of N.
   


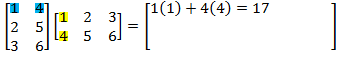
4. To find the element at a _1,2, find the matrix product of the first row of M and the second column of N


5. 


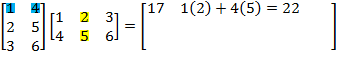
6. Repeat until each row of M has been multiplied by each column of N.
   

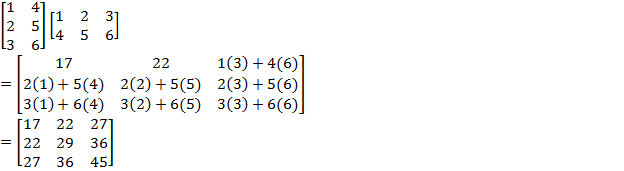
Try these exercises:

Instructions

1. 
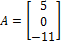
   Find 7A.


2. 
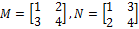
   Find 2M-2N.


3. 
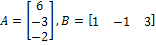
   Find BA.


4. 
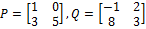
   Find PQ.


5. 
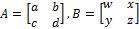
   Find AB and BA, then compare the results to show that matrix multiplication is not commutative for 2*2 matrices.


6. 
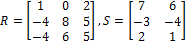
   Find RS.


7. 
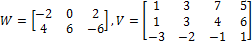
   Find WV


8. Can the product of a 2*2 matrix and a 2*4 matrix be multiplied by a 4*2 matrix? Why or why not?


9. The matrix product
   
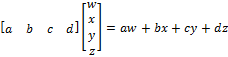
   Reverse this procedure to express -2x+3y+z as a matrix product.


10. 
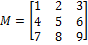
    Find MI₃

Answers to questions:

1. 


2. 


3. 


4. 


5. 
   
   
   
   


6. 


7. 


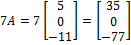
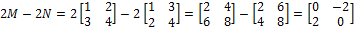
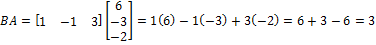
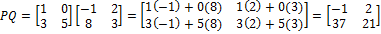
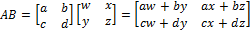
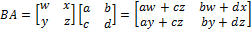
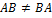
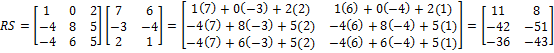
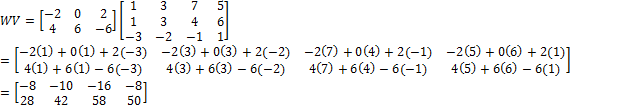
8. The product of the 2*2 matrix and the 2*4 matrix will have dimension 2*4 (2*22*4). This matrix and the 4*2 matrix can be multiplied because the first matrix has the same number of columns (4) as the second has rows (2*44*2). They can also be multiplied in the opposite order (4*22*4).


9. 


10.