The Principle of Mathematical Induction

We will now learn about one of the most powerful tools of mathematics; the principle of mathematical induction. Its uses are manifold in all branches of mathematics. Some basic laws of addition and multiplication can be proved using this principle.

The principle for mathematical induction

{ p(n) | n ∈ N} is a set of statements. If p(1) is true, p(k) is true

⇒ p(k + 1) is true

and is (ii) true for p(k) ⇒ p(k + 1) is true and whenever it is true

for 1, 2, . . , n. then the statement p(n) is true for all natural numbers n.

Let us prove the following statement using the principle of mathematical induction.

Example

1. Prove that 1+ 3 + 5 + . . . + (2n – 1) = n²
   Solution: We use the principle of induction on n. The statement p(n) is:
        1+ 3 + 5 + . . . + (2n – 1) = n²
        Clearly p(1) is true because 1 = 1²   ——————   ( i )
        Assume that the statement is true for k. (this is called the induction hypothesis)
         i.e. 1+ 3 + 5 + . . . + (2k – 1) = k²   ———————   ( ii )
        We have to prove the truth of p(n) for (k + 1).
        Adding 2(k + 1) – 1 = 2k + 1, the term next to 2k – 1 on both sides of (ii) we find that:
        1 + 3 + 5 + . . . + (2k – 1) + (2k + 1) = k² + (2k + 1)
         = (k + 1)²  —— (iii)
        From (i), (ii) and (iii) we can conclude that the result p(n) is true for all natural numbers.


2. Prove that p(n): n2– 79n + 1601 is a prime.
   Solution:
   p(n): n² – 79n + 1601 is a prime for n = 0, 1, 2 . . . , 79.
        But for n = 80, p(n) gives (80)² – 79 . 80 + 1601 = 412,
        a composite number. Thus p(n) is not true in general though it is true for n = 0, 1, 2, 3, . . ., 79.


3. Prove that 1 + 3 + 5 + . . . + (2n – 1) = n² + 5
   Solution: Suppose p(k) 1 + 3 + 5 + . . . + (2k – 1) = k² + 5 is true. - (1)
        Now 1 + 3 + 5 + . . . + (2k – 1) + (2k + 1) = k² + 5 + (2k + 1)
        {after adding 2k+1 to both sides of equation (1) }
                = (k + 1)² + 5
         That is p(k) is true. p(k+1)
         But this is not true for n = 1 as 1 ≠ 6
         ∴  p(n): 1 + 3 + 5 + . . . + (2n – 1) = n² + 5 is not true for all n.
   By this time you might have observed that the principle basically gives a method of proof for a known formula and it is not in itself a tool for inventing the formula.

Try these questions

I)   Using the principle of mathematical induction prove the following

1.                                    n(n + 1)
   1 + 2 + 3 + . . . + n =  —————
                                          2


2.                                               n²(n + 1)²
   1³ + 2³ + 3³ + . . . + n³  =  —————
                                                  4


3.                                              3(3n – 1)
   3 + 3² + 3³ + . . . + 3³  =  —————
                                                     2



II)    Using the principle of mathematical induction show that

4.                                                                  n(n + 1)(2n + 1)           n(n + 1)²(n + 2)
   1²+(1² + 2²) + (1² + 2² + 3²) + . . . +  ———————  =    ———————
                                                                            6                                   12


5. 3³ⁿ – 26 n – 1 is divisible by 676

Answers

I)    Using the principle of mathematical induction prove the following

1.                                    n(n + 1)
   1 + 2 + 3 + . . . + n =  —————
                                          2
   Solution:
   P(1) is true because 1(1 + 1)/2 = 1
   Assume that the statement is true for k (induction hypothesis).
   i.e. 1 + 2 + 3+ - - - +k = k(k+1) / 2 ----- (1)
   Now to prove p(k + 1) add (k + 1) on both sides of (1)
   
                                                          k(k + 1)                    (k + 1)(k + 2)
   1 + 2 + 3 + . . . + k + (k + 1) =  ———— + (k + 1)  =  ———————
                                                                2                                 2
   ∴  p(k + 1) is true
   ∴   p(n) is true for all n


2.                                              n²(n + 1)²
   1³ + 2³ + 3³ + . . . + n³  =  —————
                                                    4
   
   Solution:
                                                          n²(n + 1)²
   s(n) (2)    1³ + 2³ + 3³ + . . . + n³  =  —————
                                                                 4
                 put n = 1    L.H.S = 1³ = 1
   
                                                      1²(1 + 1)²         4
                                  R.H.S =  —————  =  ——   =   1
                                                              4               4
   
                                  L.H.S = R.H.S
   
                                                                            k²(k + 1)²
   Assume   n = k      1³+ 2³ + 3³ + . . . + k³  =  —————    (1)
                                                                                 4
   add (k + 1)³   to both sides of (1)
                                                              k²(k + 1)²               
   1³ + 2³ + 3³ + . . . + k³ + (k + 1)³ =  ———— + (k + 1)³
                                                                    4                       
   
                                                          k²(k + 1)² + (k + 1)³  
                                                     =  —————————
                                                                       4
   
                                                          (k + 1)² [k² + 4(k + 1)]  
                                                     =  ———————————
                                                                         4
                                                          (k + 1)² [k² + 4k + 1]  
                                                     =  ——————————
                                                                        4
                                                          (k + 1)² (k + 2)²  
                                                     =  ———————
                                                                   4
                                               ∴    p(k+1) is true
                                               ∴    p(n) is true for all n


3.                                         3(3n – 1)
   3 + 3² + 3² + . . . + 3²  =  —————
                                                2
   Solution:
        n = 1     L.H.S = 3¹ =3.
                    
   



II)    Using the principle of mathematical induction show that

4. 
   ∴ P (1) is true
   Let p(k) be true
   that is
   
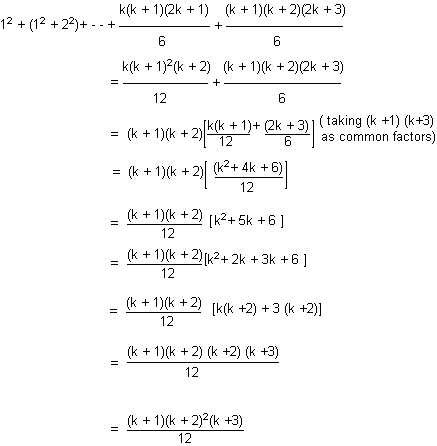
                                     ∴ S (k + 1) is true


5. 3³ⁿ – 26n – 1 is divisible by 676
   Solution:
            s(n) = 3³ⁿ– 26n – 1
            n =1   3^{3 (1)} – 26(1) – 1
                   = 3³ – 26 – 1
                   = 27 – 27 = 0    which is divisible by 676
            s(1) is true
            s(k) = 33 * 26k – 1
   Let 3 ^3k - 26k - 1  = 676 p ----- (1)                [where p is integer]
   ⇒ Consider s(k+1)
                     3 (k+1)
   s(k+1) = 3 - 26(k+1) - 1
             =3^3k * 33 - 26k - 26 - 1
             =3^3k + 26k * 3^3k - 26 - 1
             =(3^3k -26k -1) + 26 * 3^3k - 26 ------------(2)
   From (1) 3^3k = 676p + 26k +1
   Substituting in (2)
   s(k+1) = 676P + 26 ( 676p + 26K + 1) -26
             =676P + 26 ( 676p + 26K + 1 - 1)
             =676 + 26 ( 676p + 26K )
             =676p + 26 (26) [26p + k] as 676 = 26²
             =676p + 676 (26p + k)
             =676 [p + 26p + k] =676 (27p + K)
        ⇒  =3^{3 (k+1)} - 26 (k+1) - 1 is divisible by 676
   ∴ s (k + 1 ) is true