Characteristics and mantissa of a logarithm

Consider the following.

We will take logs to the base 10 as we are dealing with common logarithms.

From the above cases, it is clear that the logarithm of a number increases as the number increases and decreases as the number decreases. It also follows that if a number lies between 0 and 10, its logarithm lies between 0 and 1. If the number lies between 10 and 100, the logarithm lies between 1 and 2, and so on.

So, the logarithm of a number is partly integral (that is, it is an integer) and partly fractional.

The integral part of a logarithm is called the characteristic and the fractional or decimal part of the logarithm is called the mantissa.

Rule for determining the characteristic of a common logarithm

Example 1:

Number	Integral Digits N	Characteristic n-1
1657	4	3
208	3	2
56.7	2	1
81	2	1
97.3614	2	1
8.4123	1	0
6	1	0

If N, the given number, is less than 1; that is, it is a fraction or decimal and contains the first significant figures after n zeros (for example, in .0000561 the significant figures are 561 after four zeros) immediately after the decimal point, then as stated earlier it follows that a decimal fraction with no zero immediately following the decimal point lies between 10^-1 and 10⁰ (for example, 0.34). A decimal fraction with one zero following immediately after the decimal point lies between 10^-2 and 10^-1 (for example, 0.0519), etc.

or log N = -(n+1) + a proper fraction

Thus, the characteristic of the logarithm of a decimal fraction N with n zeros following the decimal point is -(n+1).

Example 2

with the same significant figures.

For example, the mantissa for

1) 3125, 31.25, 3.125, 0.3125 and .0003125 have the same mantissa, although their characteristics are different.

Example 3

If the mantissa of 5813 is .7644

write the logs of

a. 5813000        b. 5.813        c. 0.0005813        d. 58.13

Given that the mantissa of log 5813 = .7644

1. 581300
   Number of integral digits = 6
   Characteristic of log = n-1 = 6-1 = 5
   log 581300 = 5 + .7644
                    = 5.7644


2. 5.813
   Number of integral digits = 1
   Characteristic = n-1 = 1-1 = 0
   log 5.813 = 0 + .7644
                 = 0.7644


3. 0.0005813
   Number of zeros after decimal point = 3
   


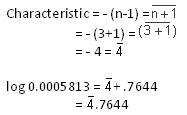
4. 58.13
   Number of integral digits = 2
   Characteristic = n-1
                        = 2-1
                        = 1
   log 58.13 = 1+ .7644
                  = 1.7644

Sometimes, we may obtain a logarithm that is wholly negative. In this case, we need to use arithmetical operations to write the logarithm so that the mantissa is positive.

Example 4

The result -2.17985 may be transformed by adding -1 to the integral part and +1 to the decimal part.

- 2.17895 = -2 -1 + (1 - .7985)

               = -3 + (0.82015)

               =

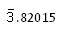
Example 5

1. Write down the characteristics of the logarithms of
   1. 3174
   2. 625.7
   3. 0.374
   4. 0.00135
   5. 1.26 * 10^-10


2. The Mantissa of log 37203 is .5705. Write down the logs of
   1. 37.203
   2. 3.7203
   3. 372030000
   4. .000037203
   5. .37203


3. The logarithm of 7623 is 3.8821. Write down the numbers whose logarithms are
   


4. Given log 2 = .3010, log 3 = .4771, log 7 = .8451. Find the number of digits or zeros in
   


5. Given log 2 = .3010 and log 3 = .4771. Find the numerical value of x in the following equations.
   

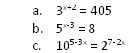
Answers to problems

1. 1. Number = 3174
      Number of integral digits = n = 4
      Characteristic = n-1 = 4-1
      = 3
   
   
   2. Number = 625.7
      Number of integral digits = n = 3
      Characteristic = n-1
      = 3-1
      = 2
   
   
   3. Number = 0.374
      
   
   
   4. Number = 0.00135
      
   
   
   5. Number = 1.26 * 10-10
      


2. Mantissa of log 37203 is .5705
   


3. The logarithm of 7623 is 3.8821
   1. To write the number whose log is 0.8821
      log 7623 = 3.8821
      Let log x = 0.8821
             Characteristic = 0
      ⇒ the number has a single digit
      ∴ x = 7.623
   
   
   2. 
   
   
   3. To write the number whose log is 7.8821 log 7623 = 3.8821
      Let log x = 7.8821
             Characteristic = 7
      ⇒ number of integral digits = 7+1 = 8
      ∴ x = 76230000
   
   
   4. To write the number whose log is 1.8821
      log 7623 = 3.8821
      Let log x = 1.8821
             Characteristic of x = 1
      ⇒ number of integral digits = 1+1 = 2
      ∴ x = 76.23
   
   


4. 1. Given log 2 = .3010, log 3 = .4771, log 7 = .8451. Find the number of digits in (42)⁴²
      Solution:
      
   
   
   2. Given log 2 = .3010, log 3 = .4771, and log 7 = .8451. Find the number of digits in (81/80)¹⁰⁰⁰
      Solution:
      


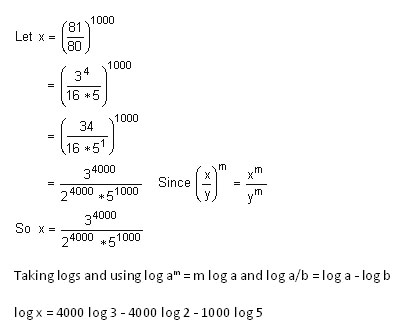
5. 1. Given log 2 = .3010 and log 3 = .4771. Find the numerical value of x in 3x+2 = 405
      
   
   
   2. Given log 2 = .3010, log 3 = .4771 to obtain a numerical value for x
      5^x-3 = 8
      5^x-3 = 2³
      Taking logs and using log a^m = m log a
      (x-3) log 5 = 3 log 2
      xlog 5 - 3 log 5 = 3 log 2
      x log 5 = 3 log 2+ 3 log 5