Definition of an ellipse
An ellipse is the locus of a point that moves in the plane in such a way that the ratio of its distance from a fixed point in the same plane to its distance from a fixed straight line is always constant and is always less than unity.
The constant ratio is denoted by e and is known as the eccentricity of the ellipse.
If S is the focus, ZZ1 is the directrix and P is any point on the ellipse, then the definition
SP/PM = e
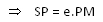
Example 1
Find the equation of the ellipse whose focus is (1, 0) and directrix is x + y + 1 = 0.
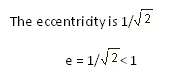
Let S(1, 0) be the focus, ZZ1 be the directrix and the point P(x,y) be any point on the ellipse.
PM = perpendicular from P onto the directrix then
SP/PM = e
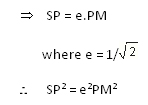

Try these questions
1. Find the equation of the ellipse where
a. |
Focus is (-1, 1) Directrix x - 2y + 3= 0 and e = 1/3 |
b. |
Focus is (-2, 3) Directrix is 2x + 3y + 4 = 0, e = 4/5 |
c. |
Focus is (1, 2) Directrix is 3x + 4y - 5 = 0, e = 1/2 |
Answers
a. Solution



b. Solution
Given that the focus S = (-2,3)
Directrix is 2x + 3y + 4= 0
e = 4/5
If P(x,y) is a point on the ellipse
PM = perpendicular from P onto the directrix

Cross-multiplying
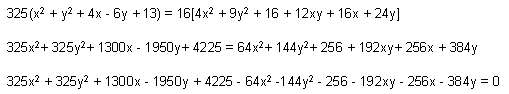
c. Solution
Focus = (1, 2) = S
Directrix is 3x + 4y - 5 = 0
Eccentricity e = 1/2
If P(x,y) be a point on the ellipse
PM = perpendicular from P onto the directrix
