Definition of the different types of conic sections and their equations

A conic section or conic is the locus of a point P that moves in such a way that its distance from a fixed point S always bears a common ratio to its distance from a fixed line, all being in the same plane.

Definitions of various important terms

Focus

The fixed point S is called the focus of the conic section.

Directrix

The fixed straight line is called the directrix of the conic section.

Eccentricity

The constant ratio is called the eccentricity of the conic section and is generally denoted by e.

1. If e = 0 the conic is a circle
2. If e < 1 the conic is an ellipse
3. If e = 1 the conic is a parabola
4. If e > 1 the conic is a hyperbola

Axis

The straight line passing through the focus and perpendicular to the directrix is called the axis of the conic section.

Vertex

The points of intersection of the conic section and the axis are called the vertices of the conic section.

Center

The point that bisects every chord passing through it is called the center of the conic section.

Latus Rectum

The latus rectum of a conic is the chord passing through the focus and perpendicular to the axis.

General equation of a conic section with given focus, directrix and eccentricity

Let S = (h, k) be the focus

Ax + By + C = 0 be the directrix

e = eccentricity

of the conic.

Let P( x1, y1) be any point on the conic.

Let PM be the perpendicular from P on the directrix. Then, by definition

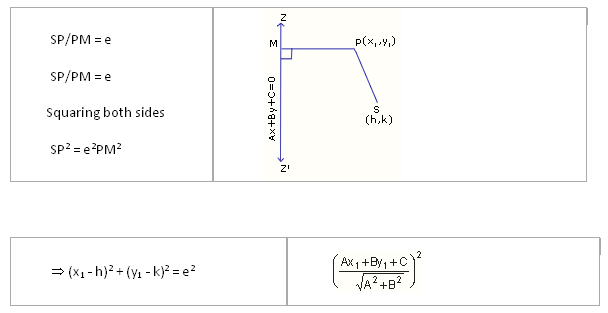
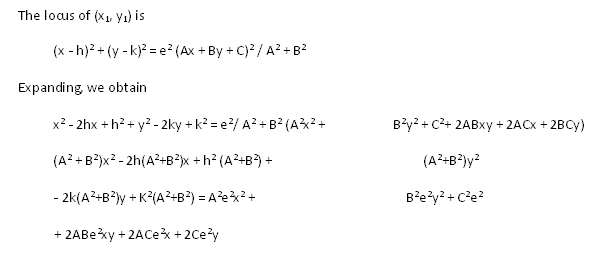
Collecting like terms together,

is also called the discriminant.

Example 1

Consider the following equations. State which equation is a circle, parabola, ellipsis and hyperbola.

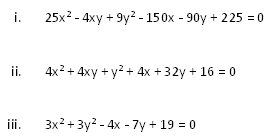
i)   Solutions

ii)   Solutions

iii)   Solutions

Try this question